题目内容
15.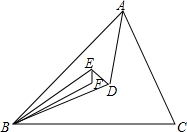 如图,△ABC内一点D,AD、BD、CD分别平分∠A、∠B、∠C,又E是△ABD内一点,AE、BE、CE分别平分△ABD各内角,F为△BDE内一点,BF、EF、DF分别平分△BDE各内角.若∠BFE的度数为整数,则∠BFE至少是113°度.
如图,△ABC内一点D,AD、BD、CD分别平分∠A、∠B、∠C,又E是△ABD内一点,AE、BE、CE分别平分△ABD各内角,F为△BDE内一点,BF、EF、DF分别平分△BDE各内角.若∠BFE的度数为整数,则∠BFE至少是113°度.
分析 先证明∠ADB=90°+$\frac{1}{2}$∠C,由此可以得到∠BFE=112.5°+$\frac{1}{8}$∠C即可解决问题.
解答  解:如图,∵AD、BD是△ABC内角平分线,BF、EF、DF分别平分△BDE各内角,
解:如图,∵AD、BD是△ABC内角平分线,BF、EF、DF分别平分△BDE各内角,
∴∠ADB=180°-$\frac{1}{2}$(∠ABC+∠BAC)=180°-$\frac{1}{2}$(180°-∠C)=90°+$\frac{1}{2}$∠C,
同理:∴∠BFE=90°+$\frac{1}{2}$∠BDE=90°+$\frac{1}{4}$(90°+$\frac{1}{2}$∠C)=112.5°+$\frac{1}{8}$∠C,
∴∠BFE>112.5°,
∵∠BFE的度数为整数,
∴∠BFE的度数至少为113°.
点评 本题考查三角形内角和定理、角平分线的性质,解题的关键是记住结论∠ADB=90°+$\frac{1}{2}$∠C,这个结论是中考常考知识点,理解整数、至少的含义.

练习册系列答案
相关题目
7.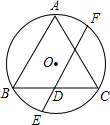 如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥AB,若AB=8,则DE的长为( )
如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥AB,若AB=8,则DE的长为( )
 如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥AB,若AB=8,则DE的长为( )
如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥AB,若AB=8,则DE的长为( )| A. | $\sqrt{5}$+1 | B. | 2$\sqrt{5}$-2 | C. | 2$\sqrt{3}$-2 | D. | $\sqrt{3}$+1 |
5.下列说法中,正确的是( )
| A. | 如果a2=b2,那么a=b | B. | 如果ac=bc,那么a=b | ||
| C. | 如果a=b,那么2a+c=b+2c | D. | 如果a-c=b-c,那么a=b |
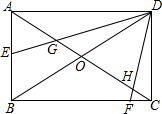 已知:如图,在矩形ABCD中,∠EDF两边分别与边AB、BC交于E、F,与对角线交于G、H,且∠EDF=∠BDC,∠BDC=60°,AE=2,DH=$\sqrt{13}$时,DG=$\frac{4\sqrt{13}}{3}$.
已知:如图,在矩形ABCD中,∠EDF两边分别与边AB、BC交于E、F,与对角线交于G、H,且∠EDF=∠BDC,∠BDC=60°,AE=2,DH=$\sqrt{13}$时,DG=$\frac{4\sqrt{13}}{3}$.