题目内容
1．
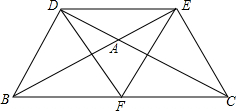如图，在△ABC中，∠BAC＞90°，DC⊥DB，BE⊥EC，F为BC上的一个动点，猜想：当F为于BC上的什么位置时，△FDE是等腰三角形，并证明你的猜想是正确的．
分析 根据直角三角形斜边上的中线等于斜边的一半进行解答．
解答 当F为BC上的中点时，△FDE是等腰三角形，
证明：∵DC⊥DB，F为BC上的中点，
∴DF=$\frac{1}{2}$BC，
∵BE⊥EC，F为BC上的中点，
∴EF=$\frac{1}{2}$BC，
∴DF=EF，
∴△FDE是等腰三角形．
点评 本题考查的是直角三角形的性质，掌握直角三角形斜边上的中线等于斜边的一半是解题的关键．
练习册系列答案
相关题目
如图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如果大正方形的面积是13，小正方形的面积是1，那么每个直角三角形的周长为$5+\sqrt{13}$．
9．如果a2+3a+k分解后有一个因式为（a-1），那么k的值（ ）
| A． | 6 | B． | -6 | C． | -4 | D． | -5 |
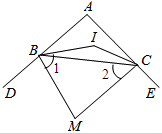如图，△ABC中，∠A=α，BI、CI分别平分∠ABC，∠ACB，则∠BIC=90°+$\frac{α}{2}$，若BM、CM分别为∠ABC，∠ACB的外角平分线，则∠M=90°-$\frac{α}{2}$．
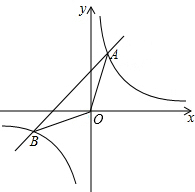如图，一次函数y1=x+2的图象与反比例函数y2=$\frac{k}{x}$（k为常数，且k≠0）的图象都经过点A，B，其中点A的坐标为（1，m）．
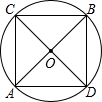如图所示，AB，CD是⊙O的两条相互垂直的直径．