题目内容
6.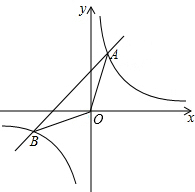 如图,一次函数y1=x+2的图象与反比例函数y2=$\frac{k}{x}$(k为常数,且k≠0)的图象都经过点A,B,其中点A的坐标为(1,m).
如图,一次函数y1=x+2的图象与反比例函数y2=$\frac{k}{x}$(k为常数,且k≠0)的图象都经过点A,B,其中点A的坐标为(1,m).(1)求点A的坐标及反比例函数的解析式;
(2)连接OA,OB,求△OAB的面积.
分析 (1)先将A(1,m)代入一次函数y1=x+2,求出m=3,再将A(1,3)代入反比例函数y2=$\frac{k}{x}$,运用待定系数法即可求出反比例函数的解析式;
(2)先根据解析式求出B点坐标,设一次函数y1=x+2与y轴交于点C,得出C的坐标,再根据△AOB的面积=△AOC的面积+△COB的面积即可求解.
解答 解:(1)∵一次函数y1=x+2的图象经过点A(1,m),
∴m=1+2=3,
∴A(1,3),
代入反比例函数y2=$\frac{k}{x}$得,k=3,
∴反比例函数的解析式为y2=$\frac{3}{x}$;
(2)解$\left\{\begin{array}{l}{y=x+2}\\{y=\frac{3}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$,
∴B(-3,-1),
设一次函数y1=x+2与y轴交于点C,
∴C点坐标为(0,2),
∴△AOB的面积=△AOC的面积+△COB的面积
=$\frac{1}{2}$×2×1+$\frac{1}{2}$×2×3
=1+3
=4.
点评 此题主要考查了反比例函数和一次函数的交点问题,待定系数法求函数的解析式,三角形的面积等知识,难度适中,体现了数形结合的思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

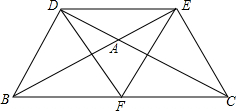 如图,在△ABC中,∠BAC>90°,DC⊥DB,BE⊥EC,F为BC上的一个动点,猜想:当F为于BC上的什么位置时,△FDE是等腰三角形,并证明你的猜想是正确的.
如图,在△ABC中,∠BAC>90°,DC⊥DB,BE⊥EC,F为BC上的一个动点,猜想:当F为于BC上的什么位置时,△FDE是等腰三角形,并证明你的猜想是正确的.