题目内容
13.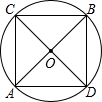 如图所示,AB,CD是⊙O的两条相互垂直的直径.
如图所示,AB,CD是⊙O的两条相互垂直的直径.(1)四边形ACBD是什么四边形?为什么?
(2)若⊙O的直径为4cm,求四边形ACBD的面积.
分析 (1)由已知条件得出OA=OB,OC=OD,AB=CD,得出四边形ACBD是矩形,再由对角线互相垂直得出四边形ABCD是菱形,即可得出四边形ACBD是正方形;
(2)由正方形的性质得出四边形ACBD的面积等于两条对角线长积的一半,即可得出结果.
解答 解:(1)四边形ACBD是正方形;理由如下:
∵AB,CD是⊙O的两条相互垂直的直径,
∴OA=OB,OC=OD,AB=CD,AB⊥CD,
∴四边形ACBD是平行四边形,
∴四边形ACBD是矩形,
∵AB⊥CD,
∴四边形ABCD是菱形,
∴四边形ACBD是正方形;
(2)∵AB=CD=4cm,AB⊥CD,四边形ACBD是正方形,
∴四边形ACBD的面积=$\frac{1}{2}$AB•CD=$\frac{1}{2}$×4×4=8(cm2).
点评 本题考查了正方形与圆、正方形的判定与性质、矩形、菱形的判定方法;熟练掌握正方形的判定与性质,证明四边形是正方形是解决问题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
3.如图所示的三个矩形中,其中相似形是( )


| A. | 甲与乙 | B. | 乙与丙 | C. | 甲与丙 | D. | 以上都不对 |
2.一元一次方程$\frac{x}{1×2}$+$\frac{x}{2×3}$+$\frac{x}{3×4}$+…+$\frac{x}{2015×2016}$=2015的解是( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
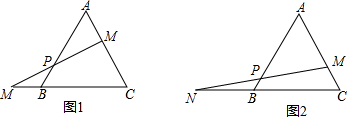
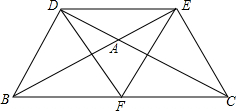 如图,在△ABC中,∠BAC>90°,DC⊥DB,BE⊥EC,F为BC上的一个动点,猜想:当F为于BC上的什么位置时,△FDE是等腰三角形,并证明你的猜想是正确的.
如图,在△ABC中,∠BAC>90°,DC⊥DB,BE⊥EC,F为BC上的一个动点,猜想:当F为于BC上的什么位置时,△FDE是等腰三角形,并证明你的猜想是正确的.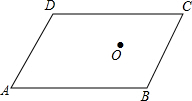 如图,O是?ABCD内一点,以O为位似中心,作?ABCD的位似图形,使?ABCD的边长缩小到原来的$\frac{1}{2}$.
如图,O是?ABCD内一点,以O为位似中心,作?ABCD的位似图形,使?ABCD的边长缩小到原来的$\frac{1}{2}$.