题目内容
12.Rt△ABC的三边分别为a,b,c,且a2+b2+c2=200,则斜边c=10.分析 直接利用勾股定理得出a2+b2=c2,进而得出c的值.
解答 解:∵Rt△ABC的三边分别为a,b,c,且a2+b2+c2=200,
∴a2+b2=c2=100,
∴斜边c=10.
故答案为:10.
点评 此题主要考查了勾股定理,得出a2+b2=c2是解题关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
3.如图所示的三个矩形中,其中相似形是( )


| A. | 甲与乙 | B. | 乙与丙 | C. | 甲与丙 | D. | 以上都不对 |
20.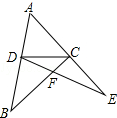 如图,△ABC、△ADE中,C、D两点分别在AE、AB上,BC与DE相交于F点.若BD=CD=CE,∠ADC+∠ACD=104°,则∠DFC的度数为( )
如图,△ABC、△ADE中,C、D两点分别在AE、AB上,BC与DE相交于F点.若BD=CD=CE,∠ADC+∠ACD=104°,则∠DFC的度数为( )
 如图,△ABC、△ADE中,C、D两点分别在AE、AB上,BC与DE相交于F点.若BD=CD=CE,∠ADC+∠ACD=104°,则∠DFC的度数为( )
如图,△ABC、△ADE中,C、D两点分别在AE、AB上,BC与DE相交于F点.若BD=CD=CE,∠ADC+∠ACD=104°,则∠DFC的度数为( )| A. | 104° | B. | 118° | C. | 128° | D. | 136° |
2.一元一次方程$\frac{x}{1×2}$+$\frac{x}{2×3}$+$\frac{x}{3×4}$+…+$\frac{x}{2015×2016}$=2015的解是( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
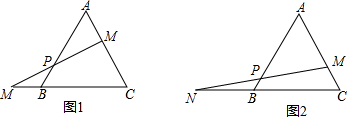
 如图,在△ABC中,∠BAC>90°,DC⊥DB,BE⊥EC,F为BC上的一个动点,猜想:当F为于BC上的什么位置时,△FDE是等腰三角形,并证明你的猜想是正确的.
如图,在△ABC中,∠BAC>90°,DC⊥DB,BE⊥EC,F为BC上的一个动点,猜想:当F为于BC上的什么位置时,△FDE是等腰三角形,并证明你的猜想是正确的.