题目内容
如图，下列推理错误的是（ ）| A、∵∠1=∠2，∴a∥b |
| B、∵∠1=∠3，∴a∥b |
| C、∵∠3=∠5，∴c∥d |
| D、∵∠2+∠4=180°，∴c∥d |
考点：平行线的判定
专题：计算题
分析：根据直线平行的判定定理即可判断．
解答：解：A、根据内错角相等，两直线平行即可证得，故结论正确；
B、错误；
C、同位角相等，两直线平行，结论正确；
D、同旁内角互补，两直线平行，结论正确．
故选B．
B、错误；
C、同位角相等，两直线平行，结论正确；
D、同旁内角互补，两直线平行，结论正确．
故选B．
点评：正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
如图，阴影部分组成的图案既是关于x轴成轴对称的图形，又是关于坐标原点O成中心对称的图形．若点A的坐标为（1，3），则点M和点N的坐标分别为M
如图，△ABC经过平移后到达△A′B′C′的位置，那么平移的方向是三角形的三条中位线的长分别为3cm，4cm，5cm，则原三角形的周长为（ ）
| A、6.5cm | B、24cm |
| C、26cm | D、52cm |
“a＞b”的反面是（ ）
| A、a＜b | B、a≠b |
| C、a=b | D、a=b或a＜b |
已知线段AB及AB上一点P，当点P满足下列哪一种关系时，点P为AB的黄金分割点：
①AP2=AB•PB；②AP=
AB；③PB=
AB；④
=
；⑤
=
．
其中正确的是（ ）
①AP2=AB•PB；②AP=
| ||
| 2 |
3-
| ||
| 2 |
| AP |
| PB |
| ||
| 2 |
| AB |
| AP |
| ||
| 2 |
其中正确的是（ ）
| A、①②③ | B、①②③④ |
| C、②③④⑤ | D、①②③④⑤ |
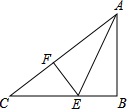如图，AE为∠BAC的平分线，EB⊥AB，EF⊥AC，则下列结论不正确的是（ ）| A、EF=EB |
| B、AF=AB |
| C、AE=CE |
| D、∠AEF=∠AEB |