题目内容
如图，ACB是直线，AB⊥CD，EC⊥FC，图中共有（ ）对角互余．| A、2 | B、3 | C、4 | D、以上都不对 |
考点：余角和补角
专题：
分析：余角：如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角．
解答：解：∵AB⊥CD，EC⊥FC，
∴∠ACE与∠DCE互余，∠BCF与∠DCF互余，∠DCE与∠DCF互余，
∴∠ACE与∠BCF互余，
共有4对角互余．
故选：C．
∴∠ACE与∠DCE互余，∠BCF与∠DCF互余，∠DCE与∠DCF互余，
∴∠ACE与∠BCF互余，
共有4对角互余．
故选：C．
点评：此题综合考查垂直，余角和补角．在找互余或互余的两角时，可先确定较小（或较大）角的度数，从最小（或最大）角的补角（或余角）开始找，能做到不重合、不遗漏．
练习册系列答案
相关题目
如图，阴影部分组成的图案既是关于x轴成轴对称的图形，又是关于坐标原点O成中心对称的图形．若点A的坐标为（1，3），则点M和点N的坐标分别为M“a＞b”的反面是（ ）
| A、a＜b | B、a≠b |
| C、a=b | D、a=b或a＜b |
已知线段AB及AB上一点P，当点P满足下列哪一种关系时，点P为AB的黄金分割点：
①AP2=AB•PB；②AP=
AB；③PB=
AB；④
=
；⑤
=
．
其中正确的是（ ）
①AP2=AB•PB；②AP=
| ||
| 2 |
3-
| ||
| 2 |
| AP |
| PB |
| ||
| 2 |
| AB |
| AP |
| ||
| 2 |
其中正确的是（ ）
| A、①②③ | B、①②③④ |
| C、②③④⑤ | D、①②③④⑤ |
计算（-a2）3•（-a3）2的结果是（ ）
| A、a12 |
| B、-a12 |
| C、-a10 |
| D、-a36 |
下列各数不能与1，3，
成比例的是（ ）
| 2 |
A、3
| ||||
B、
| ||||
C、
| ||||
D、
|
如图的图案中，是轴对称图形的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
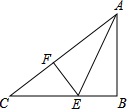如图，AE为∠BAC的平分线，EB⊥AB，EF⊥AC，则下列结论不正确的是（ ）| A、EF=EB |
| B、AF=AB |
| C、AE=CE |
| D、∠AEF=∠AEB |
如图，在⊙O中，直径AB⊥弦CD于点E．若BE=