题目内容
某个玻璃饰品的外形是简单多面体,它的外表由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为x,八边形的个数为y,求x+y的值.
考点:认识立体图形
专题:
分析:根据欧拉公式可得顶点数+面数-棱数=2,然后表示出棱数,进而可得面数.
解答:解:∵有24个顶点,每个顶点处都有3条棱,两点确定一条直线;
∴共有24×3÷2=36条棱,
设总面数为F,
24+F-36=2,
解得F=14,
∴x+y=14.
∴共有24×3÷2=36条棱,
设总面数为F,
24+F-36=2,
解得F=14,
∴x+y=14.
点评:此题主要考查了欧拉公式,关键是掌握顶点数+面数-棱数=2.

练习册系列答案
相关题目
从O点看,射线OA在是北偏西60°方向上,射线OB在南偏东15°方向上,那么∠AOB的度数为( )
| A、45° | B、75° |
| C、90° | D、135° |
 如图,小明同学在南北方向的滨河路A处,测得体育馆P在北偏西30°方向上,向北前行500米到达B处,测得体育馆P在北偏西75°方向上,求体育馆P到滨河路的距离PC.(结果精确到0.1米,
如图,小明同学在南北方向的滨河路A处,测得体育馆P在北偏西30°方向上,向北前行500米到达B处,测得体育馆P在北偏西75°方向上,求体育馆P到滨河路的距离PC.(结果精确到0.1米, 已知,如图,⊙O1与坐标轴交于A(1,0),B(5,0)两点,点O1的纵坐标为5,求⊙O1的半径.
已知,如图,⊙O1与坐标轴交于A(1,0),B(5,0)两点,点O1的纵坐标为5,求⊙O1的半径. 如图,AB、CD交于点O,∠AOE=90°,若∠AOC:∠COE=5:4,求∠AOD的度数.
如图,AB、CD交于点O,∠AOE=90°,若∠AOC:∠COE=5:4,求∠AOD的度数.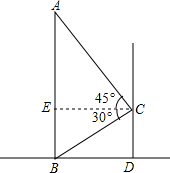 如图所示,某中学的教学楼前有一棵大树AB,小明在教学楼的C处测得树顶A的仰角为45°,底部B的俯角为30°,已知大树与教学楼之间的水平距离BD=6m,求AB(结果保留根号).
如图所示,某中学的教学楼前有一棵大树AB,小明在教学楼的C处测得树顶A的仰角为45°,底部B的俯角为30°,已知大树与教学楼之间的水平距离BD=6m,求AB(结果保留根号). 直线AB,CD被直线EF所截,交AB,CD于点M,N,NH是一条射线,图中共有多少对同位角?多少对内错角?多少对同旁内角?分别指出这些角?
直线AB,CD被直线EF所截,交AB,CD于点M,N,NH是一条射线,图中共有多少对同位角?多少对内错角?多少对同旁内角?分别指出这些角? 如图,A、B、C、D是圆上的点,∠1=70°,∠A=40°,求∠D.
如图,A、B、C、D是圆上的点,∠1=70°,∠A=40°,求∠D.