题目内容
对某校毕业生进行体检，前50名学生中有49名合格，以后每8名中有7名合格，且该校毕业生体检合格率在90%以上，则该校毕业生人数最多是（ ）
| A、180 | B、200 |
| C、210 | D、225 |
考点：用样本估计总体
专题：
分析：该校毕业生体检合格率就是合格总人数所占毕业生总人数的百分比；再根据不等式的意义求出该校毕业生人数的最大值．
解答：解：∵以后每8名中有7名是合格的，
∴设除去前50名学生以外，还有以“8名学生为一小组”的小团体的个数为x，
则合格学生为49+7x，毕业生总人数为50+8x，
∴校毕业生体检合格率=
×100%≥90%，
解得x≤20．
根据题意，x最大值为20．
∴该校毕业生人数最多为：50+8×20=210（人）．
故选C．
∴设除去前50名学生以外，还有以“8名学生为一小组”的小团体的个数为x，
则合格学生为49+7x，毕业生总人数为50+8x，
∴校毕业生体检合格率=
| 49+7x |
| 50+8x |
解得x≤20．
根据题意，x最大值为20．
∴该校毕业生人数最多为：50+8×20=210（人）．
故选C．
点评：此题主要考查了利用一般估计总体的思想，弄清合格率的含义和毕业生合格人数与毕业生总人数的表示方法是解决此题的关键所在．要合理设未知数和熟练运用不等式的知识．
练习册系列答案
相关题目
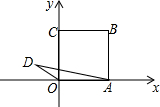如图所示：OABC是正方形，OD∥AC．|AD|=|AC|，若|OA|=1，则D的坐标是（ ）A、（
| ||||||||
B、（
| ||||||||
C、（
| ||||||||
D、（
|
定义新运算△为：a△b=ab+2a+2b+2，如果x△2△2△2△2△2=5118，则x=（ ）
| A、1 | B、2 | C、3 | D、无法确定 |
用长度为2l的材料围成一个矩形场地，中间有2个隔墙，要使矩形的面积最大，则隔墙的长度为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、l |
方程x2+4x+k=0有两个实根x1和x2，且（x12+4x1）（x22+4x2）=25，则k的值是（ ）
| A、±5 | B、5 |
| C、-5 | D、不存在这样的k值 |