题目内容
2.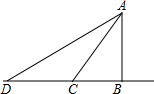 如图,某学校A与直线公路BD的距离AB为3km,与该公路上一车站D相距5km,现要在公路边建一个小商店C,使之与学校A及车站D的距离相等,请你推算一下,该商店应建在距车站D多远处.
如图,某学校A与直线公路BD的距离AB为3km,与该公路上一车站D相距5km,现要在公路边建一个小商店C,使之与学校A及车站D的距离相等,请你推算一下,该商店应建在距车站D多远处.
分析 根据题意,AC=CD,∠ABD=90°,由AB、AD的长易求BD,设CD=x米,则AC=x,BC=BD-x.在直角三角形ABC中运用勾股定理得关系式求解.
解答 解;设CD的距离为xkm,则AC=CD=xkm,
在Rt△ABD中,BD=$\sqrt{A{D}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4(km).
CB=BD-CD=(4-x)km,
在Rt△ABC中,AC2=AB2+BC2,
即x2=32+(4-x)2.
解得x=3.125.
答:该商店应建在距车站D3.125km处.
点评 本题考查了勾股定理的应用.图中有两个直角三角形,只有边的关系,只能运用勾股定理求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.在π,$\frac{17}{8}$,-$\sqrt{7}$,$\root{3}{125}$,3.1415,0.3,-$\frac{{\sqrt{5}}}{3}$,-3.20202020…,4.1818818881…中,有理数的个数有( )
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
12.已知a>b,则下列不等式中,正确的是( )
| A. | -3a>-3b | B. | -$\frac{a}{3}>-\frac{b}{3}$ | C. | 3-a<3-b | D. | a-3<b-3 |
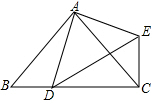 如图,在△ABC中,AB=AC,点D在线段BC上运动,连接AD,以AD为边作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
如图,在△ABC中,AB=AC,点D在线段BC上运动,连接AD,以AD为边作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.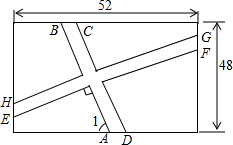 要在一块长52m,宽48m的矩形绿地上修建同样宽的两条互相垂直的甬路.下面是小颖的设计方案,如图所示,BC=HE=2,AB∥CD,HG∥EF,AB⊥EF,∠1=60°,求小颖设计方案中四块绿地的总面积.
要在一块长52m,宽48m的矩形绿地上修建同样宽的两条互相垂直的甬路.下面是小颖的设计方案,如图所示,BC=HE=2,AB∥CD,HG∥EF,AB⊥EF,∠1=60°,求小颖设计方案中四块绿地的总面积.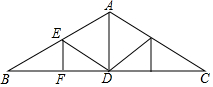 如图是屋顶的“人字形”钢架,其中斜梁AB=AC,顶角∠BAC=120°,立柱AD⊥BC,EF⊥BC,DE∥AC,AB=8m,则EF=2m.
如图是屋顶的“人字形”钢架,其中斜梁AB=AC,顶角∠BAC=120°,立柱AD⊥BC,EF⊥BC,DE∥AC,AB=8m,则EF=2m.