题目内容
8．求f（x）=x2+$\frac{1}{{x}^{2}}$的最小值．分析 根据配方法可以求得题目中式子的最小值．
解答 解：f（x）=x2+$\frac{1}{{x}^{2}}$=（x-$\frac{1}{x}$）2+2，
∴当x=1时，f（x）取得最小值，此时f（x）=2，
即f（x）=x2+$\frac{1}{{x}^{2}}$的最小值是2．
点评 本题考查二次根式的最值，解答本题的关键是明确题意，求出相应的式子的最值．
练习册系列答案
相关题目
已知：如图，在梯形ABCD中，AD∥BC，AB=DC，点E、F、G分别在边AB、BC、CD上，AE=GF=GC 
如图，平行四边形ABCD中，E为AB的中点，连接AC，DE相交于点F，若△AEF的面积等于1，则△ACD的面积是6．
16．把一团圆柱体橡皮泥揉成与它等底的圆锥体，高将（ ）
| A． | 扩大3倍 | B． | 缩小3倍 | C． | 扩大6倍 | D． | 缩小6倍 |
13．
定义：如图，点M、N把线段AB分割成AM、MN和BN，若以AM、MN、BN为边的三角形构成一个直角三角形，则称点M、N是线段AB的勾股分割点，若AM=2，MN=3，则BN的长为（ ）
定义：如图，点M、N把线段AB分割成AM、MN和BN，若以AM、MN、BN为边的三角形构成一个直角三角形，则称点M、N是线段AB的勾股分割点，若AM=2，MN=3，则BN的长为（ ）| A． | $\sqrt{5}$ | B． | $\sqrt{13}$ | C． | $\sqrt{5}$或$\sqrt{13}$ | D． | 无法确定 |
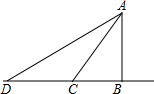如图，某学校A与直线公路BD的距离AB为3km，与该公路上一车站D相距5km，现要在公路边建一个小商店C，使之与学校A及车站D的距离相等，请你推算一下，该商店应建在距车站D多远处．