题目内容
9．
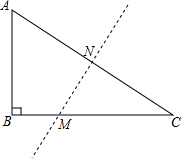如图，在Rt△ABC中，∠B=90°，AC=10，AB=6，沿直线MN对折后，点C恰好与点A重合，试求MB的长．
分析 连接AM，先利用勾股定理求得BC=8，然后由翻折的性质得到AM=MC，设BM=x，则MC=AM=8-x，最后在Rt△ABM中利用勾股定理列方程求解即可．
解答 解：连接AM．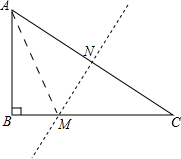
在Rt△ABC中，由勾股定理得：BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8．
由翻折的性质可知：AM=MC．
设BM=x，则MC=AM=8-x．
在Rt△ABM中由勾股定理得：AM2=AB2+BM2，即（8-x）2=x2+62，
解得：x=$\frac{7}{4}$．
则MB=$\frac{7}{4}$．
点评 本题主要考查的是翻折的性质、勾股定理的应用，在Rt△ABM中由勾股定理列出关于x的方程是解题的关键．
练习册系列答案
相关题目
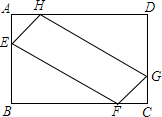如图，在矩形ABCD中，AB=6，BC=8，点E、F、G、H分别在边AB、BC、CD、AD上，且AE=AH=CF=CG，设AE的长为x，四边形EFGH的面积为S．