题目内容
19.有一种房梁的截面积是一个矩形,且矩形的长与宽之比为$\sqrt{3}$:1,现用直径为3$\sqrt{15}$cm的一种圆木做原料加工这种房梁,那么加工后的房梁的最大截面积是多少?分析 首先确定直径,然后根据长宽之比设出长和宽,然后利用勾股定理建立方程求得长和宽,从而求得最大面积.
解答 解:如图,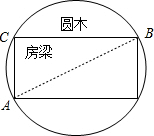
AB为圆木的直径,
∵矩形的长与宽之比为$\sqrt{3}$:1,
∴设矩形的长为$\sqrt{3}$x,宽为x,
由勾股定理得:AC2+BC2=AB2,
即:($\sqrt{3}$x)2+x2=(3$\sqrt{15}$)2,
解得:x=$\frac{3\sqrt{15}}{2}$,
∴AC=$\frac{3\sqrt{15}}{2}$cm,BC=$\frac{9\sqrt{5}}{2}$cm,
∴房梁的最大面积为$\frac{3\sqrt{15}}{2}$×$\frac{9\sqrt{5}}{2}$=$\frac{135\sqrt{3}}{4}$cm2.
点评 此题考查一元二次方程的实际运用,勾股定理,建立直角三角形是解决问题的关键.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
10.下列方程为一元一次方程的是( )
| A. | 2x-3=y | B. | x2-2x-3=0 | C. | x=0 | D. | $\frac{1}{y}$-1=y |
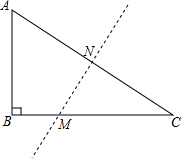 如图,在Rt△ABC中,∠B=90°,AC=10,AB=6,沿直线MN对折后,点C恰好与点A重合,试求MB的长.
如图,在Rt△ABC中,∠B=90°,AC=10,AB=6,沿直线MN对折后,点C恰好与点A重合,试求MB的长.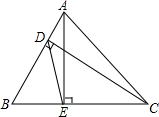 在△ABC中,CD,AE分别为AB、BC边上的高,∠B=60°,求证:DE=$\frac{1}{2}$AC.
在△ABC中,CD,AE分别为AB、BC边上的高,∠B=60°,求证:DE=$\frac{1}{2}$AC.