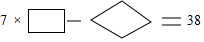
题目内容
17. 已知Rt△ABC纸片的两直角边长分别为6,8,现将△ABC如图所示那样折叠,使点A与点B重合,则BE的长是( )
已知Rt△ABC纸片的两直角边长分别为6,8,现将△ABC如图所示那样折叠,使点A与点B重合,则BE的长是( )| A. | $\frac{25}{4}$ | B. | $\frac{15}{4}$ | C. | $\frac{25}{2}$ | D. | $\frac{15}{2}$ |
分析 根据勾股定理求出AB,根据翻转变换的性质得到EA=EB,BD=AD=5,证明△ADE∽△ACB,根据相似三角形的性质列出比例式,计算即可.
解答 解:由勾股定理得,AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=10,
由翻转变换的性质可知,EA=EB,BD=AD=5,
∵∠ADE=∠C=90°,∠A=∠A,
∴△ADE∽△ACB,
∴$\frac{AD}{AC}$=$\frac{AE}{AB}$,即$\frac{5}{8}$=$\frac{AE}{10}$,
解得,AE=$\frac{25}{4}$,
故选:A.
点评 本题主要考查了翻折变换的性质、相似三角形的判定和性质,解题的关键是折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
8.点M(-3,2)关于y轴对称的点的坐标为( )
| A. | (-3,-2) | B. | (3,-2) | C. | (-3,2) | D. | (3,2) |
2.圆内接四边形ABCD中,已知∠A=70°,则∠C等于( )
| A. | 110° | B. | 70° | C. | 30° | D. | 20° |
9.已知⊙O的半径为1,圆心O的坐标为(0,0),点P的坐标为($\sqrt{2}$,-1),则点P与⊙O的位置关系是( )
| A. | 点P在⊙O内 | B. | 点P在⊙O上 | C. | 点P在⊙O外 | D. | 点P在⊙O上或⊙O外 |
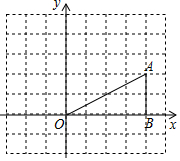 如图,在平面直角坐标系中,已知点A(4,2),B(4,0).
如图,在平面直角坐标系中,已知点A(4,2),B(4,0).