题目内容
9.已知⊙O的半径为1,圆心O的坐标为(0,0),点P的坐标为($\sqrt{2}$,-1),则点P与⊙O的位置关系是( )| A. | 点P在⊙O内 | B. | 点P在⊙O上 | C. | 点P在⊙O外 | D. | 点P在⊙O上或⊙O外 |
分析 根据点到圆心的距离与圆的半径之间的关系:“点到圆心的距离为d,则当d=r时,点在圆上;当d>r时,点在圆外;当d<r时,点在圆内”来求解.
解答 解:OP=$\sqrt{(\sqrt{2})^{2}+(-1)^{2}}$=$\sqrt{3}$,
d=$\sqrt{3}$.
d>r,
点P在⊙O外,
故选:C.
点评 本题考查了对点与圆的位置关系的判断.设点到圆心的距离为d,则当d=r时,点在圆上;当d>r时,点在圆外;当d<r时,点在圆内.

练习册系列答案
相关题目
20. 如图,点I是三角形ABC的内心,连接AI并延长交BC于点E,交三角形ABC的外接圆于点D,连接BD.
如图,点I是三角形ABC的内心,连接AI并延长交BC于点E,交三角形ABC的外接圆于点D,连接BD.
(1)若∠BAC=70°,∠D=40°,求∠CED的度数;
(2)试问BD与ID相等吗?为什么?
 如图,点I是三角形ABC的内心,连接AI并延长交BC于点E,交三角形ABC的外接圆于点D,连接BD.
如图,点I是三角形ABC的内心,连接AI并延长交BC于点E,交三角形ABC的外接圆于点D,连接BD.(1)若∠BAC=70°,∠D=40°,求∠CED的度数;
(2)试问BD与ID相等吗?为什么?
17. 已知Rt△ABC纸片的两直角边长分别为6,8,现将△ABC如图所示那样折叠,使点A与点B重合,则BE的长是( )
已知Rt△ABC纸片的两直角边长分别为6,8,现将△ABC如图所示那样折叠,使点A与点B重合,则BE的长是( )
 已知Rt△ABC纸片的两直角边长分别为6,8,现将△ABC如图所示那样折叠,使点A与点B重合,则BE的长是( )
已知Rt△ABC纸片的两直角边长分别为6,8,现将△ABC如图所示那样折叠,使点A与点B重合,则BE的长是( )| A. | $\frac{25}{4}$ | B. | $\frac{15}{4}$ | C. | $\frac{25}{2}$ | D. | $\frac{15}{2}$ |
4. 实数a,b在数轴上的位置如图所示,以下说法正确的是( )
实数a,b在数轴上的位置如图所示,以下说法正确的是( )
 实数a,b在数轴上的位置如图所示,以下说法正确的是( )
实数a,b在数轴上的位置如图所示,以下说法正确的是( )| A. | a+b=0 | B. | ab>0 | C. | b<a | D. | |b|<|a| |
14.若二次函数y=ax2+b的图象经过点P(-2,4),则下列各点中,一定在该图象上的是( )
| A. | (-4,2) | B. | (4,-2) | C. | (2,4) | D. | (-2,-4) |

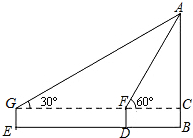 某同学利用测角仪及卷尺测量某校旗杆的高度,在测量中获得了一些数据,并以此画出了如图所示的示意图,已知该同学使用的测角仪(离地面的高度)支杆长1m,第一次在D处测得旗杆顶端A的仰角为60°,第二次向后退12m到达E处,又测到旗杆顶端A的仰角为30°,求旗杆的高度.(结果保留根号)
某同学利用测角仪及卷尺测量某校旗杆的高度,在测量中获得了一些数据,并以此画出了如图所示的示意图,已知该同学使用的测角仪(离地面的高度)支杆长1m,第一次在D处测得旗杆顶端A的仰角为60°,第二次向后退12m到达E处,又测到旗杆顶端A的仰角为30°,求旗杆的高度.(结果保留根号)