题目内容
在△ABC中，∠B的平分线为BD，DE∥AB交BC于点E，若AB=9，BC=6，求S△DCE：S四边形ABED．
考点：相似三角形的判定与性质
专题：
分析：由∠B的平分线为BD和DE∥AB可得DE=BE，且△CDE∽△CAB，
=
，设CE=x，则DE=BE=6-x，代入可求得DE的长，即可求得相似比，可求出S△DCE：S△CAB，进一步可求出S△DCE：S四边形ABED．
| DE |
| AB |
| CE |
| CB |
解答：解：
∵∠B的平分线为BD，
∴∠ABD=∠EBD，
∵DE∥AB，
∴∠EDB=∠ABD，
∴∠EBD=∠EDB，
∴DE=BE，
∵DE∥AB，
∴△CDE∽△CAB，
∴
=
，
设CE=x，则DE=BE=6-x，
∴
=
，解得x=2.4，
∴DE=3.6，
∴
=
=
=
，
∴
=
，
整理可求得S△DCE：S四边形ABED=2：3．
∵∠B的平分线为BD，
∴∠ABD=∠EBD，
∵DE∥AB，
∴∠EDB=∠ABD，
∴∠EBD=∠EDB，
∴DE=BE，
∵DE∥AB，
∴△CDE∽△CAB，
∴
| DE |
| AB |
| CE |
| CB |
设CE=x，则DE=BE=6-x，
∴
| 6-x |
| 9 |
| x |
| 6 |
∴DE=3.6，
∴
| S△CED |
| S△CAB |
| DE |
| AB |
| 3.6 |
| 9 |
| 2 |
| 5 |
∴
| S△CED |
| S△CED+S四边形ABED |
| 2 |
| 5 |
整理可求得S△DCE：S四边形ABED=2：3．
点评：本题主要考查相似三角形的性质，解题的关键是利用条件求得相似三角形的相似比．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
如图，四边形ABCD是⊙O的内接四边形，且AC⊥BD，OF⊥AB，垂足分别为E、F，请问OF与CD有怎样的数量关系？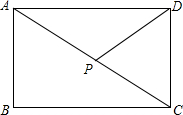
如图，矩形ABCD中，AB=3，BC=4，点P是对角线AC上的动点（不与A、C重合），设AP=x，S△CDP=y．