题目内容
 如图,四边形ABCD是⊙O的内接四边形,且AC⊥BD,OF⊥AB,垂足分别为E、F,请问OF与CD有怎样的数量关系?
如图,四边形ABCD是⊙O的内接四边形,且AC⊥BD,OF⊥AB,垂足分别为E、F,请问OF与CD有怎样的数量关系?考点:三角形中位线定理,圆心角、弧、弦的关系,圆周角定理
专题:
分析:连接AO并延长,与⊙O相交于点G,连接BG,根据同弧所对的圆周角相等可得∠G=∠ADB,再根据等角的余角相等求出∠DAE=∠BAG,然后根据相等的圆周角所对的弦相等可得CD=BG,根据垂径定理可得AF=BF,从而得到OF是△ABG的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得OF=
BG.
| 1 |
| 2 |
解答: 解:OF=
解:OF=
CD.
理由如下:如图,连接AO并延长,与⊙O相交于点G,连接BG,
则∠G=∠ADB,
∵AC⊥BD,
∴∠DAE+∠ADB=90°,
∵AG是直径,
∴∠BAG+∠G=90°,
∴∠DAE=∠BAG,
∴CD=BG,
∵OF⊥AB,
∴AF=BF,
∴OF是△ABG的中位线,
∴OF=
BG,
故OF=
CD.
 解:OF=
解:OF=| 1 |
| 2 |
理由如下:如图,连接AO并延长,与⊙O相交于点G,连接BG,
则∠G=∠ADB,
∵AC⊥BD,
∴∠DAE+∠ADB=90°,
∵AG是直径,
∴∠BAG+∠G=90°,
∴∠DAE=∠BAG,
∴CD=BG,
∵OF⊥AB,
∴AF=BF,
∴OF是△ABG的中位线,
∴OF=
| 1 |
| 2 |
故OF=
| 1 |
| 2 |
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,圆周角定理,圆心角、弧、弦的关系,作辅助线构造出以OF为中位线的三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
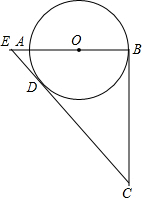 如图所示,CB、CD分别切圆心O于点B、D,AB为圆心O的直径,延长BA交CD的延长线于点E,求证:ED•EC=EO•EB.
如图所示,CB、CD分别切圆心O于点B、D,AB为圆心O的直径,延长BA交CD的延长线于点E,求证:ED•EC=EO•EB. 如图,D是△ABC的BC边上的一点,且∠2=∠BAC,试说明∠1=∠B.
如图,D是△ABC的BC边上的一点,且∠2=∠BAC,试说明∠1=∠B.