题目内容
抛物线y=x2+(2m+1)x+m2-1,x∈R.
(1)求证:不论m为何值,函数图象顶点都在同一直线L1上;
(2)求证:任一平行L1且与抛物线相交的直线,被各抛物线截得的线段长相等.
(1)求证:不论m为何值,函数图象顶点都在同一直线L1上;
(2)求证:任一平行L1且与抛物线相交的直线,被各抛物线截得的线段长相等.
考点:二次函数的性质
专题:证明题
分析:(1)把原抛物线解析式配成顶点式得到抛物线顶点坐标为(-m-
,-m-
),由于横纵坐标之差为常数,则可判断点(-m-
,-m-
)在直线x-y=
上,
(2)设与L1:y=x-
平行的直线为y=x+b,根据两函数图象的交点问题得到
,消去y得x2+2mx+m2-1-b=0,利用根与系数的关系表示出两交点的横坐标之差,再利用直线的性质得到两交点的距离等于两横坐标之差的绝对值的
倍,而表示线段长的代数式与m无关,只与b有关,于是可判断任一平行L1且与抛物线相交的直线,被各抛物线截得的线段长相等.
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
| 3 |
| 4 |
(2)设与L1:y=x-
| 3 |
| 4 |
|
| 2 |
解答:证明:(1)∵y=x2+(2m+1)x+m2-1
=(x+m+
)2+m-
,
∴抛物线顶点坐标为(-m-
,-m-
),
∵-m-
-m+
=
∴点(-m-
,-m-
)在直线x-y=
上,
即不论m为何值,函数图象顶点都在同一直线y=x-
上;
(2)设与L1:y=x-
平行的直线为y=x+b,
∴
,
∴x2+2mx+m2-1-b=0,
设直线y=x+b与抛物线的交点的横坐标分别为p、q,则p+q=-2m,pq=m2-1-b=0,
∴|p-q|=
=
=2
,
∵直线y=x+b与x轴正方向的交角为45°,
∴直线y=x+b被各抛物线截得的线段长为
|p-q|=2
,
此线段长只与b有关,
∴任一平行L1且与抛物线相交的直线,被各抛物线截得的线段长相等.
=(x+m+
| 1 |
| 2 |
| 5 |
| 4 |
∴抛物线顶点坐标为(-m-
| 1 |
| 2 |
| 5 |
| 4 |
∵-m-
| 1 |
| 2 |
| 5 |
| 4 |
| 3 |
| 4 |
∴点(-m-
| 1 |
| 2 |
| 5 |
| 4 |
| 3 |
| 4 |
即不论m为何值,函数图象顶点都在同一直线y=x-
| 3 |
| 4 |
(2)设与L1:y=x-
| 3 |
| 4 |
∴
|
∴x2+2mx+m2-1-b=0,
设直线y=x+b与抛物线的交点的横坐标分别为p、q,则p+q=-2m,pq=m2-1-b=0,
∴|p-q|=
| (p+q)2-4pq |
| 4+4b |
| b+1 |
∵直线y=x+b与x轴正方向的交角为45°,
∴直线y=x+b被各抛物线截得的线段长为
| 2 |
| 2b+2 |
此线段长只与b有关,
∴任一平行L1且与抛物线相交的直线,被各抛物线截得的线段长相等.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
相关题目
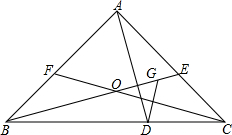 如图,在等腰△ABC中,AB=AC,∠BAC=90°,AE=AF,BE、CF交于点O,过A作BE的垂线交BC于D,过D作CF的垂线交BE于G.
如图,在等腰△ABC中,AB=AC,∠BAC=90°,AE=AF,BE、CF交于点O,过A作BE的垂线交BC于D,过D作CF的垂线交BE于G.