题目内容
12.按如图所示的程序流程计算,若开始输入的值为x=3,则最后输出的结果是21.
分析 根据程序可知,输入x,计算出$\frac{x(x+1)}{2}$的值,若值小于20,然后再其值作为x,输入代数式,直到结果大于20即可.
解答 解:∵当x=3时,$\frac{3×(3+1)}{2}$=6<20;
当x=6时,$\frac{6×(6+1)}{2}$=21>20,
∴最后输出的结果是21.
故答案为:21.
点评 此题考查的是代数式求值,解答本题的关键就是弄清楚题图给出的计算程序.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
3.如果关于x的一元二次方程mx2+x+m=0有两个实数根,那么( )
| A. | 两根互为相反数 | B. | 两根相等 | C. | 两根互为倒数 | D. | 两根和为1 |
7.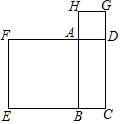 如图,矩形ABCD的周长是20cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为68cm2,那么矩形ABCD的面积是( )
如图,矩形ABCD的周长是20cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为68cm2,那么矩形ABCD的面积是( )
 如图,矩形ABCD的周长是20cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为68cm2,那么矩形ABCD的面积是( )
如图,矩形ABCD的周长是20cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为68cm2,那么矩形ABCD的面积是( )| A. | 9cm2 | B. | 16cm2 | C. | 21cm2 | D. | 24cm2 |
17.下列句子属于命题的是( )
| A. | a2<0(a为实数) | B. | 将16开平方 | C. | 钝角大于90°吗? | D. | 取线段AB的中点 |
1.关于x的不等式组$\left\{\begin{array}{l}3x-1>4({x-1})\\ x<a\end{array}\right.$的解集为x<3,那么a的取值范围为( )
| A. | a>3 | B. | a≥3 | C. | a<3 | D. | a≤3 |
2.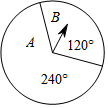 如图,让转盘自由转动一次,则指针落在A区域的概率是( )
如图,让转盘自由转动一次,则指针落在A区域的概率是( )
 如图,让转盘自由转动一次,则指针落在A区域的概率是( )
如图,让转盘自由转动一次,则指针落在A区域的概率是( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
 如图所示,∠B=90°,求x的值.
如图所示,∠B=90°,求x的值.