题目内容
20.当m取何值时,等式$\frac{x+3}{2x-1}$=$\frac{(x+3)(3m+2)}{(2x-1)(7-2m)}$成立?分析 根据分式的基本性质进行计算即可.
解答 解:∵$\frac{x+3}{2x-1}$=$\frac{(x+3)(3m+2)}{(2x-1)(7-2m)}$,
∴3m+2=7-2m,且3m+2≠0,
∴m=1,
∴当m=1时,等式$\frac{x+3}{2x-1}$=$\frac{(x+3)(3m+2)}{(2x-1)(7-2m)}$成立.
点评 本题考查了分式的值本性质,掌握分式的基本性质是解题的关键.

练习册系列答案
相关题目
11.下列计算正确的是( )
| A. | 45.5°=45°30′ | B. | 3a+b=3ab | C. | -$\frac{1}{2}$>-$\frac{1}{3}$ | D. | a3+a2=a5 |
9.下列事件哪个是必然事件( )
| A. | 任意抛掷一枚图钉,结果针尖朝上 | |
| B. | 任意抛掷一枚均匀的骰子,骰子停止转动后,朝上的一面的点数为1 | |
| C. | 连结⊙O的一条弦的中点和圆心的直线垂直这条弦 | |
| D. | 在一张纸上画两个三角形,这两个三角形相似 |
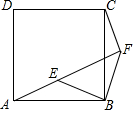 如图,点E是正方形ABCD内一点,将△ABE绕点B顺时针旋转90°到△CBF的位置,点A,E,F恰好在同一直线上.
如图,点E是正方形ABCD内一点,将△ABE绕点B顺时针旋转90°到△CBF的位置,点A,E,F恰好在同一直线上.