题目内容
4.(1)求不等式5(x-2)+8<3x+7的最大整数解.(2)解不等式组$\left\{\begin{array}{l}3x-2>4x\\ \frac{1+5x}{2}≥\frac{3x-1}{3}\end{array}\right.$.
分析 (1)先去括号、移项、合并同类项得到后把x的系数化为1得到x<8.5,然后找出此范围中的最大整数即可;
(2)分别解两个不等式得到x<-2和x≥-$\frac{5}{9}$,然后根据大大小小找不到确定不等式组的解集.
解答 解:(1)5x-10<3x+7,
5x-3x<10+7,
2x<17,
x<8.5,
所以不等式的最大整数解为8;
(2)$\left\{\begin{array}{l}{3x-2>4x①}\\{\frac{1+5x}{2}≥\frac{3x-1}{3}②}\end{array}\right.$
解①得x<-2,
解②得x≥-$\frac{5}{9}$,
所以不等式组无解.
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
14.在直角△ABC中,AC=6,E在AC边上,满足CE=2AE,D为斜边AB的中点,F是线段BC上一动点,满足∠EDF=90°,则BF-FC的最大值是( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
19.下列命题的逆命题正确的是( )
| A. | 全等三角形对应角相等 | B. | 对顶角相等 | ||
| C. | 全等三角形对应边相等 | D. | 若a=b,则|a|=|b| |
9.下列事件哪个是必然事件( )
| A. | 任意抛掷一枚图钉,结果针尖朝上 | |
| B. | 任意抛掷一枚均匀的骰子,骰子停止转动后,朝上的一面的点数为1 | |
| C. | 连结⊙O的一条弦的中点和圆心的直线垂直这条弦 | |
| D. | 在一张纸上画两个三角形,这两个三角形相似 |
16.不等式2x-1<3的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
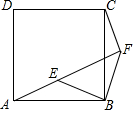 如图,点E是正方形ABCD内一点,将△ABE绕点B顺时针旋转90°到△CBF的位置,点A,E,F恰好在同一直线上.
如图,点E是正方形ABCD内一点,将△ABE绕点B顺时针旋转90°到△CBF的位置,点A,E,F恰好在同一直线上.
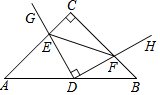 在 Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG,DH分别与边AC,BC交于E,F两点.下列结论①AE+BF=$\frac{{\sqrt{2}}}{2}$AB,②AE2+BF2=EF2,③S四边形CEDF=$\frac{1}{2}$S△ABC,④△DEF始终为等腰直角三角形.其中正确的是( )
在 Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG,DH分别与边AC,BC交于E,F两点.下列结论①AE+BF=$\frac{{\sqrt{2}}}{2}$AB,②AE2+BF2=EF2,③S四边形CEDF=$\frac{1}{2}$S△ABC,④△DEF始终为等腰直角三角形.其中正确的是( )