题目内容
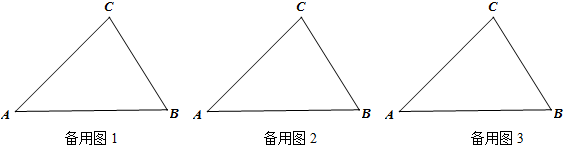
6. 如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证:
如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证:(1)AF=CG;
(2)DG=CF;
(3)直接写出CF与DE的数量关系.
分析 (1)要证AF=CG,只需证明△AFC≌△CBG即可;
(2)连接AG,证明△ACG≌△BCG,得出AG=BG,再证出∠D=∠GAD,得出AG=DG,从而证出DG=CF;
(3)延长CG交AB于H,则CH⊥AB,H平分AB,继而证得CH∥AD,得出DG=BG和△ADE与△CGE全等,从而证得CF=2DE.
解答 证明:(1)∵∠ACB=90°,AC=BC,CG平分∠ACB,
∴∠CAF=∠CBA=45°,∠BCG=∠ACG=45°,
∴∠BCG=∠CAF=45° ∵∠CBG=∠ACF,AC=BC
∵∠CBG=∠ACF,AC=BC
∴△BCG≌△CAF,
∴AF=CG;
(2)连接AG,如图1所示:
在△ACG与△BCG中,$\left\{\begin{array}{l}{AC=BC}\\{∠ACG=∠BCG}\\{CG=CG}\end{array}\right.$,
∴△ACG≌△BCG,
∴AG=BG,
∴∠GBA=∠GAB,
∵AD⊥AB
∴∠D=90°-∠GBA=90°-∠GAB=∠GAD,
∴AG=DG.
∵由(1)BG=CF,
∴DG=CF;
(3)如图2,延长CG交AB于H,
∵CG平分∠ACB,AC=BC,
∴CH⊥AB,CH平分AB,
∵AD⊥AB,
∴AD∥CG,
∴∠D=∠EGC,
在△ADE与△CGE中,
$\left\{\begin{array}{l}{∠AED=∠CEG}\\{∠D=∠EGC}\\{AE=CE}\end{array}\right.$,
∴△ADE≌△CGE(AAS),
∴DE=GE, 即DG=2DE,
即DG=2DE,
∵AD∥CG,CH平分AB,
∴DG=BG,
∵△AFC≌△CBG,
∴CF=BG,
∴CF=2DE.
点评 本题考查了三角形全等的判定和性质、等腰三角形的性质、平行线的判定及性质,三角形全等是解本题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
16.某商店出售剃须刀和刀片,在新年之际举行促销活动,每把剃须刀可盈利30元,但每个刀片亏本0.5元,在这次促销活动中,该商店售出的刀片数是剃须刀数的2倍,两种商品共获利5800元,设售出的剃须刀为x把,则可列得的一元一次方程为( )
| A. | 0.5×2x+30x=5800 | B. | 0.5x+2×30x=5800 | ||
| C. | -0.5×2x+30x=5800 | D. | 0.5×2x-30x=5800 |
15.已知点A(m+2,3m-6)在第一象限角平分线上,则m的值为( )
| A. | 2 | B. | -1 | C. | 4 | D. | -2 |
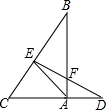 如图,在△ABC中,∠BAC=90°,BC的垂直平分线交BC于点E,交CA的延长线于D,交AB于点F,求证:AE2=EF•ED.
如图,在△ABC中,∠BAC=90°,BC的垂直平分线交BC于点E,交CA的延长线于D,交AB于点F,求证:AE2=EF•ED. 如图,C、D是线段上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则BD的长为7cm.
如图,C、D是线段上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则BD的长为7cm.