题目内容
18.已知函数y=$\frac{1}{3}$x3+2,不画图象,解答下列问题:(1)判断A(0,2)、B(2,0)、C($\root{3}{9}$,-1)三点是否在该函数图象上,说明理由;
(2)若点P(a,0)、Q(-$\sqrt{3}$,b)都在该函数的图象上,试求a、b的值.
分析 (1)分别将A,B,C点代入函数关系式进而判断即可;
(2)分别将P,Q点代入函数关系式进而得出答案.
解答 解:(1)当x=0时,y=2,
当x=2时,y=$\frac{8}{3}$+2=$\frac{14}{3}$,
当x=$\root{3}{9}$时,y=5,
故B,C点不在该函数图象上,A点在该函数图象上;
(2)当y=0时,0=$\frac{1}{3}$x3+2,
即0=$\frac{1}{3}$a3+2,
解得;a=$\root{3}{-6}$,
当x=-$\sqrt{3}$时,b=$\frac{1}{3}$×(-$\sqrt{3}$)3+2,
解得:b=2-$\sqrt{3}$.
点评 此题主要考查了函数关系式以及函数图象上点的坐标性质,正确理解图象上点的坐标性质是解题关键.

练习册系列答案
相关题目
8.已知点M(2,-3),点N与点M关于x轴对称,则点N的坐标是( )
| A. | (-2,3) | B. | (-2,-3) | C. | (3,2) | D. | (2,3) |
9.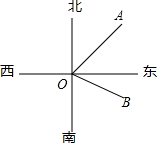 如图,在灯塔O处观测到轮船A位于东北方向,同时轮船B在南偏东55°方向,那么∠AOB的大小为( )
如图,在灯塔O处观测到轮船A位于东北方向,同时轮船B在南偏东55°方向,那么∠AOB的大小为( )
 如图,在灯塔O处观测到轮船A位于东北方向,同时轮船B在南偏东55°方向,那么∠AOB的大小为( )
如图,在灯塔O处观测到轮船A位于东北方向,同时轮船B在南偏东55°方向,那么∠AOB的大小为( )| A. | 80° | B. | 90° | C. | 100° | D. | 85° |
3.已知x2yn与-xmy3是同类项,则m+n=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
 如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证:
如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证: