题目内容
15.若关于x的一元二次方程kx2-$\sqrt{2k+3}$x+1=0有实数根,则k的取值范围是-$\frac{3}{2}$≤k≤$\frac{3}{2}$且k≠0.分析 根据一元二次方程的定义、根的判别式以及二次根式的意义列出k的不等式组,求出k的取值范围即可.
解答 解:∵一元二次方程kx2-$\sqrt{2k+3}$x+1=0有实数根,
∴$\left\{\begin{array}{l}{k≠0}\\{2k+3≥0}\\{△=2k+3-4k≥0}\end{array}\right.$
解得-$\frac{3}{2}$≤k≤$\frac{3}{2}$且k≠0,
故答案为-$\frac{3}{2}$≤k≤$\frac{3}{2}$且k≠0.
点评 本题主要考查了根的判别式的知识,解题的关键是掌握根据题意得出k≠0和△≥0,解题还要注意二次根式有意义的条件.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
6.若$\frac{3}{2}$是方程2x=3的惟一解,则x=$\frac{1}{2}$是不等式2x<3的( )
| A. | 惟一解 | B. | 一个根 | C. | 一个解 | D. | 解集 |
7.某工厂大门是抛物线形水泥建筑物,大门宽为4m,顶部距地面的高度为4.4m,现有一辆满载货物的汽车欲通过大门,其装货宽度为2.4m,该车要想通过此门,装货后的最大高度应为( )
| A. | 2.80m | B. | 2.816m | C. | 2.82m | D. | 2.826m |
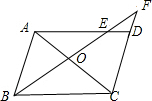 如图,平行四边形ABCD中,过B点作直线交AC、AD于O、E,交CD的延长线于F点,
如图,平行四边形ABCD中,过B点作直线交AC、AD于O、E,交CD的延长线于F点, 如图,△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC和∠ACB的平分线,点O为BD、CE的交点,则图中等腰三角形的个数是( )
如图,△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC和∠ACB的平分线,点O为BD、CE的交点,则图中等腰三角形的个数是( )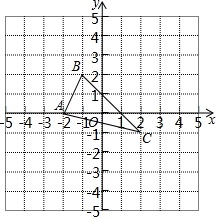 如图,在平面直角坐标系中,△ABC的三个顶点坐标是A(-2,0),B(-1,2),C(2,-1),△ABC关于x轴对称的图形是△A1B1C1.
如图,在平面直角坐标系中,△ABC的三个顶点坐标是A(-2,0),B(-1,2),C(2,-1),△ABC关于x轴对称的图形是△A1B1C1.