题目内容
4.解不等式(1)8x-1≥5x-6
(2)-3(x+2)-1<5-2(x-2)
(3)解不等式2(1-2x)≥$\frac{2x-1}{3}$-1,并把解集在数轴上表示出来.
分析 (1)根据解一元一次不等式基本步骤:移项、合并同类项、系数化为1可得;
(2)根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得.
(3)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得.
解答 解:(1)移项,得:8x-5x≥-6+1,
合并同类项,得:3x≥-5,
系数化为1,得:x≥-$\frac{5}{3}$;
(2)去括号,得:-3x-6-1<5-2x+4,
移项,得:-3x+2x<9+7,
合并同类项,得:-x<16,
系数化为1,得:x>-16;
(3)去分母,得:6-12x≥2x-1-3,
移项、合并,得:-14x≥-10,
系数化为1,得:x≤$\frac{5}{7}$,
表示在数轴上如下:
点评 本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.

练习册系列答案
相关题目
14. 一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为( )
一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为( )
 一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为( )
一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为( )| A. | 5L | B. | 3.75L | C. | 2.5L | D. | 1.25L |
14.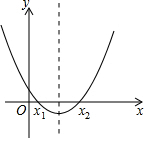 如图,函数y=x2-6x+m(m为常数)的图象如图,如果x=a时,y<0;那么x=a-6时,函数值( )
如图,函数y=x2-6x+m(m为常数)的图象如图,如果x=a时,y<0;那么x=a-6时,函数值( )
 如图,函数y=x2-6x+m(m为常数)的图象如图,如果x=a时,y<0;那么x=a-6时,函数值( )
如图,函数y=x2-6x+m(m为常数)的图象如图,如果x=a时,y<0;那么x=a-6时,函数值( )| A. | y<0 | B. | 0<y<m | C. | y=m | D. | y>m |