题目内容
13.下面是小明化简分式的过程,仔细阅读后解答所提出的问题.解:$\frac{2}{x+2}$-$\frac{x-6}{{x}^{2}-4}$-$\frac{2(x-2)}{(x+2)(x-2)}$-$\frac{x-6}{(x+2)(x-2)}$ 第一步
=2(x-2)-x+6 第二步
=2x-4-x+6 第三步
=x+2 第四步
(1)小明的解法从第二步开始出现错误;
(2)对此分式进行化简.
分析 根据分式的运算法则即可求出答案.
解答 解:(1)二
(2)原式=$\frac{2(x-2)}{(x+2)(x-2)}$-$\frac{x-6}{(x+2)(x-2)}$-$\frac{2(x-2)}{(x+2)(x-2)}$-$\frac{x-6}{(x+2)(x-2)}$
=$\frac{-2(x-6)}{(x+2)(x-2)}$
故答案为:(1)二
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
2.-8的相反数是( )
| A. | 8 | B. | -$\frac{1}{8}$ | C. | $\frac{1}{8}$ | D. | -8 |
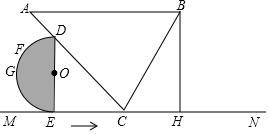 如图,∠A=45°,∠ABC=60°,AB∥MN,BH⊥MN于点H,BH=8,点C在MN上,点D在AC上,DE⊥MN于点E,半圆的圆心为点O,直径DE=6,G为$\widehat{DE}$的中点,F是$\widehat{DE}$上的动点.
如图,∠A=45°,∠ABC=60°,AB∥MN,BH⊥MN于点H,BH=8,点C在MN上,点D在AC上,DE⊥MN于点E,半圆的圆心为点O,直径DE=6,G为$\widehat{DE}$的中点,F是$\widehat{DE}$上的动点. 如图,矩形ABCD的对角线AC,BD相交于点O,若AB=3,OC=2.5,则BC长为4.
如图,矩形ABCD的对角线AC,BD相交于点O,若AB=3,OC=2.5,则BC长为4.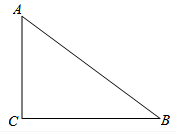 如图,已知Rt△ABC中,∠ACB=90°.请完成以下任务.
如图,已知Rt△ABC中,∠ACB=90°.请完成以下任务.