题目内容
下列多项式不能用公式法分解因式的是( )
A. 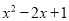 B.
B. 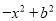 C.
C. 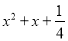 D.
D. 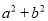
 D
【解析】根据平方差公式: ,完全平方公式: 的特点,可知:A、B、C选项可以利用完全平方公式和平方差公式进行分解因式,D选项不能利用公式法分解因式.
故选:D.
D
【解析】根据平方差公式: ,完全平方公式: 的特点,可知:A、B、C选项可以利用完全平方公式和平方差公式进行分解因式,D选项不能利用公式法分解因式.
故选:D.
练习册系列答案
相关题目
x=-1不是下列哪一个不等式的解( )
A. 2x+1≤-3 B. 2x-1≥-3 C. -2x+1≥3 D. -2x-1≤3
 A
【解析】由不等式2x+1<-3可得x<-2,所以x=-1不是不等式2x+1<-3的解;由2x-1≥-3的解集为x≥-1,可知x=-1是不等式2x+1≥-3的解;由-2x+1≥3的解集为x≤-1,可知x=-1是不等式-2x+1≥3的解;由-2x-1≤3的解集为x≥-1,可知x=-1是不等式-2x-1≤3的解.
故选:A.
A
【解析】由不等式2x+1<-3可得x<-2,所以x=-1不是不等式2x+1<-3的解;由2x-1≥-3的解集为x≥-1,可知x=-1是不等式2x+1≥-3的解;由-2x+1≥3的解集为x≤-1,可知x=-1是不等式-2x+1≥3的解;由-2x-1≤3的解集为x≥-1,可知x=-1是不等式-2x-1≤3的解.
故选:A. 下列式子能用提公因式法分解因式的是( )
A. 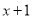 B.
B. 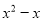 C.
C. 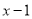 D.
D. 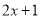
 B
【解析】根据提公因式法因式分解,可由,知B是因式分解.
故选:B.
B
【解析】根据提公因式法因式分解,可由,知B是因式分解.
故选:B. 因式分解: 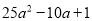 =______________
=______________
 【解析】根据完全平方公式进行因式分解为: =.
故答案为: .
【解析】根据完全平方公式进行因式分解为: =.
故答案为: . 下列哪个多项式能分解成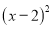 ( )
( )
A. 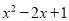 B.
B. 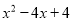 C.
C. 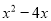 D.
D. 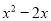
 B
【解析】根据平方差公式: ,完全平方公式: 的特点,可分解为=(x-1)2, =(x-2)2, =x(x-4),=x(x-2).
故选:B.
B
【解析】根据平方差公式: ,完全平方公式: 的特点,可分解为=(x-1)2, =(x-2)2, =x(x-4),=x(x-2).
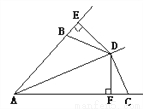
故选:B. 如图所示,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且BD=CD,那么BE与CF相等吗?为什么?
 见解析
【解析】试题分析:首先由角平分线的性质可得DE=DF,然后根据HL可证Rt△BDE≌Rt△CDF,即可证明BE=CF.
试题解析:相等.
理由是:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠DEB=∠DFC=90°,
在Rt△BDE和Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF.
见解析
【解析】试题分析:首先由角平分线的性质可得DE=DF,然后根据HL可证Rt△BDE≌Rt△CDF,即可证明BE=CF.
试题解析:相等.
理由是:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠DEB=∠DFC=90°,
在Rt△BDE和Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL),
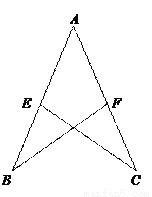
∴BE=CF. 如图,已知AB=AC=12 cm,AE=AF=7 cm,CE=10 cm,△ABF的周长是_________.
 29cm
【解析】∵AB=AC,AE=AF=7(已知),∠A=∠A(公共角)
∴△ABC≌△ACE(SAS)
∴BF=CE=10 cm,
∴△ABF的周长=AB+BF+FA=12+7+10=29(cm)
故答案为:29cm.
29cm
【解析】∵AB=AC,AE=AF=7(已知),∠A=∠A(公共角)
∴△ABC≌△ACE(SAS)
∴BF=CE=10 cm,
∴△ABF的周长=AB+BF+FA=12+7+10=29(cm)
故答案为:29cm. 已知x2+3x-1=0,求x-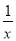 和x2+
和x2+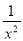 的值.
的值.
 -3,11
【解析】分析:首先将3x移项,再方程两边同除以x得出即可,再利用,方程两边同时平方求出即可.
本题解析:
因为 ,
所以 ,
将上式子两边同时除以x(x≠0),
所以 ,
,
,
则.故答案为:-3,,11.
-3,11
【解析】分析:首先将3x移项,再方程两边同除以x得出即可,再利用,方程两边同时平方求出即可.
本题解析:
因为 ,
所以 ,
将上式子两边同时除以x(x≠0),
所以 ,
,
,
则.故答案为:-3,,11. 一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.108° B.90° C.72° D.60°
 C.
【解析】
试题分析:设此多边形为n边形,根据题意得:180(n﹣2)=540,解得:n=5,故这个正多边形的每一个外角等于:360°÷5 =72°.故选C.
C.
【解析】
试题分析:设此多边形为n边形,根据题意得:180(n﹣2)=540,解得:n=5,故这个正多边形的每一个外角等于:360°÷5 =72°.故选C. 
