题目内容
下列哪个多项式能分解成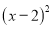 ( )
( )
A. 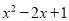 B.
B. 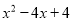 C.
C. 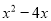 D.
D. 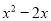
 B
【解析】根据平方差公式: ,完全平方公式: 的特点,可分解为=(x-1)2, =(x-2)2, =x(x-4),=x(x-2).
故选:B.
B
【解析】根据平方差公式: ,完全平方公式: 的特点,可分解为=(x-1)2, =(x-2)2, =x(x-4),=x(x-2).
故选:B.
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
当a ________ 时,不等式(a-1)x>1的解集是x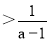
 >1
【解析】由不等式(a-1)x>1的解集是x 可知a-1>0,解得a>1.
故答案为:>1.
>1
【解析】由不等式(a-1)x>1的解集是x 可知a-1>0,解得a>1.
故答案为:>1. _____________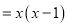
 【解析】根据整式乘法和因式分解的互逆性,可知x(x-1)=x2-x.
故答案为:x2-x.
【解析】根据整式乘法和因式分解的互逆性,可知x(x-1)=x2-x.
故答案为:x2-x. 在公式法分解因式中,有一种公式a3+b3=(a+b)(a2-ab+b2)叫立方和公式,请用它把x3+8分解因式
 (x+2)·(x2-2x+4)
【解析】试题分析:根据所给公式,将x3+8先变形为x3+23,然后套用公式,进行分解即可.
试题解析:x3+8=x3+23=(x+2)·(x2-2x+4)
(x+2)·(x2-2x+4)
【解析】试题分析:根据所给公式,将x3+8先变形为x3+23,然后套用公式,进行分解即可.
试题解析:x3+8=x3+23=(x+2)·(x2-2x+4) ______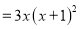
 【解析】根据因式分解与整式乘法的互逆性,可知直接进行乘法计算为: =.
故答案为: .
【解析】根据因式分解与整式乘法的互逆性,可知直接进行乘法计算为: =.
故答案为: . 下列多项式不能用公式法分解因式的是( )
A. 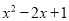 B.
B. 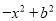 C.
C. 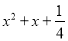 D.
D. 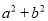
 D
【解析】根据平方差公式: ,完全平方公式: 的特点,可知:A、B、C选项可以利用完全平方公式和平方差公式进行分解因式,D选项不能利用公式法分解因式.
故选:D.
D
【解析】根据平方差公式: ,完全平方公式: 的特点,可知:A、B、C选项可以利用完全平方公式和平方差公式进行分解因式,D选项不能利用公式法分解因式.
故选:D. 已知:如图,AD是△ABC的高,E是AD上一点,BE的延长线交AC于点F,BE=AC,DE=DC,BE和AC垂直吗?说明理由.
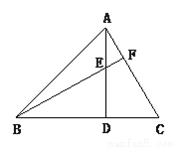
 BE⊥AC
【解析】试题分析:在直角△BED与△ACD中,根据HL判定△BED≌ACD,根据全等三角形的对应角相等,得出∠DBE=∠DAC,再根据AD是高线,结合∠BED=∠AEF,进而推出∠DAC+∠AEF=90°,据此可得结论.
试题解析:BF⊥AC.理由如下:
∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
∵在直角△BED与△ACD中,BE=AC,DE...
BE⊥AC
【解析】试题分析:在直角△BED与△ACD中,根据HL判定△BED≌ACD,根据全等三角形的对应角相等,得出∠DBE=∠DAC,再根据AD是高线,结合∠BED=∠AEF,进而推出∠DAC+∠AEF=90°,据此可得结论.
试题解析:BF⊥AC.理由如下:
∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
∵在直角△BED与△ACD中,BE=AC,DE... 如图,FE=BC,DE=AB,∠B=∠E=40°,∠F=70°,则∠A=( )
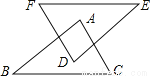
A. 40° B. 50° C. 60° D. 70°
 D
【解析】∵∠E=40°,∠F=70°,
∴∠D =70°,
∵FE=BC,DE=AB,∠B=∠E=40°,
∴△ABC≌△DEF(SAS)
∴∠A=∠D =70°.
故选:D .
D
【解析】∵∠E=40°,∠F=70°,
∴∠D =70°,
∵FE=BC,DE=AB,∠B=∠E=40°,
∴△ABC≌△DEF(SAS)
∴∠A=∠D =70°.
故选:D . 一个多边形的内角和是外角和的2倍,则这个多边形的边数为______.
 6
【解析】∵多边形的外角和是360度,多边形的内角和是外角和的2倍,
则内角和是720度,
720÷180+2=6,
∴这个多边形是六边形,
故答案为:6.
6
【解析】∵多边形的外角和是360度,多边形的内角和是外角和的2倍,
则内角和是720度,
720÷180+2=6,
∴这个多边形是六边形,
故答案为:6.