题目内容
如果△ABC中，两边a＝7cm，b＝3cm，则c的取值范围是_________；第三边为奇数的所有可能值为_________；周长为偶数的所有可能值为_________．
4cm＜c＜10cm 5cm、7cm、9cm 16cm或18cm
【解析】根据三角形的三边关系，得7cm?3cm
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案对数轴上的点P进行如下操作：先把点P表示的数乘以
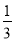，再把所得数对应的点向右平移1个单位，得到点P的对应点P′，点A，B在数轴上，对线段AB上的每个点进行上述操作后得到线段A′B′，其中点A，B的对应点分别为A′，B′，如图，若点A表示的数是﹣3，则点A′表示的数是__；若点B′表示的数是2，则点B表示的数是__．已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合，则点E表示的数是__．
0 3 1.5
【解析】试题分析：根据题目规定，以及数轴上的数向右平移用加计算即可求出点A′，设点B表示的数为a，根据题意列出方程求解即可得到点B表示的数，设点E表示的数为b，根据题意列出方程计算即可得解．
试题解析：【解析】
点A′：﹣3×+1=﹣1+1=0．
设点B表示的数为a，则a+1=2，解得a=3．
设点E表示的数为b，则b+1=b，解得b=1.5．
故答... 关于二次函数y=x2﹣2x﹣3的图象，下列说法中错误的是（ ）
A. 当x＜2，y随x的增大而减小 B. 函数的对称轴是直线x=1
C. 函数的开口方向向上 D. 函数图象与y轴的交点坐标是（0，﹣3）
A
【解析】试题分析：∵y=x2﹣2x﹣3=（x﹣1）2﹣4，
∴抛物线开口向上，对称轴为x=1，当x＜1时y随x的增大而减小，故B、C正确，A不正确，
令x=0可得y=﹣3，
∴抛物线与y轴的交点坐标为（0，﹣3），故D正确，
故选A． 已知：如图，在△ABC中有D、E两点，求证：BD＋DE＋EC＜AB＋AC．
见解析
【解析】试题分析：延长BD交AC于M点，延长CE交BD的延长线于点N．在△ABM中，AB+AM>BM，在△CNM中，NM+MC>NC，所以AB+AM+NM+MC>BM+NC，再由AM+MC=AC，BM=BN+NM可知AB+AC+NM>BN+NM+NC，故AB+AC>BN+NC，在△BNC中，BN+NC=BD+DN+NE+EC，在△DNE中，DN+NE>DE，由此即可得出结论．
... 三角形的一边上有一点，它到三个顶点的距离相等，则这个三角形是_______三角形．
直角
【解析】∵直角三角形斜边上的中线等于斜边的一半，
∴这个三角形是直角三角形.
故答案为：直角. 已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=∠A，则此三角形（ ）
A. 一定有一个内角为45° B. 一定有一个内角为60°
C. 一定是直角三角形 D. 一定是钝角三角形
C
【解析】试题解析：∵∠A+∠B+∠C=180°，∠B+∠C=∠A，
∴2∠A=180°，
∴∠A=90°，
即△ABC一定是直角三角形；
故选C． 如图，在一块边长为a的正方形纸板四周，各剪去一个边长为b(b＜0)的正方形．
(1)用代数式表示阴影部分的面积；
(2)利用因式分解的方法计算当a＝15.4，b＝3.7时，阴影部分的面积．
(1) a2－4b²;(2) 182.4.
【解析】试题分析：
试题解析：（1）用大正方形的面积减去四个小正方形的面积即可求得阴影部分的面积；（2）把所得的代数式用平方差公式因式分解后，代入求值即可.
(1)S阴影＝a2－4b2；
(2)S阴影＝(a＋2b)(a－2b)＝(15.4＋2×3.7)(15.4－2×3.7)＝22.8×8＝182.4. 已知函数y=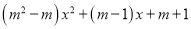
(1)若这个函数是一次函数，求m的值;
(2)若这个函数是二次函数，则m的值应怎样？
(1)、m=0；(2)、m≠0且m≠1.
【解析】试题分析：（1）由一次函数的定义求解；
（2）由二次函数的定义求解．
试题解析：（1）由一次函数的定义，得： ，解得m=0或m=1，又∵m﹣1≠0即m≠1；∴当m=0时，这个函数是一次函数；
（2）由二次函数的定义，得： ，解得且，∴当且时，这个函数是二次函数． 课外阅读课上，老师将43本书分给各小组，每组8本，还有剩余；每组9本却又不够，问有几个小组？
x＝5.
【解析】试题分析：根据题意中的不等关系，设有x个小组，列不等式组求解，然后判断出正整数解即可.
试题解析：设有x个小组，题意得，解得：＜x＜，因为x为正整数，所以x＝5.