题目内容
10.若x2-5x+2=0,则x4-3x3-7x2-x+7=5.分析 根据x2-5x+2=0,可以得到x2-5x的值,然后将所求式子变形即可解答本题.
解答 解:∵x2-5x+2=0,
∴x2-5x=-2,
∴x4-3x3-7x2-x+7
=x2(x2-5x)+2x3-7x2-x+7
=-2x2+2x3-7x2-x+7
=2x3-9x2-x+7
=2x(x2-5x)+x2-x+7
=-4x+x2-x+7
=x2-5x+7
=-2+7
=5,
故答案为:5.
点评 本题考查因式分解,解答本题的关键是找出已知式子与未知式子之间的关系,利用因式分解法解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.下列式子没有意义的是( )
| A. | $\sqrt{-(-2)}$ | B. | $\sqrt{0}$ | C. | $\sqrt{-2}$ | D. | $\sqrt{(-2)^{2}}$ |
 已知,在△ABC中,AB=AC=a,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
已知,在△ABC中,AB=AC=a,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.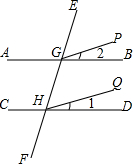 如图,已知GP平分∠EGB,HQ平分∠GHD,如果∠1=∠2,那么GP∥HQ吗?为什么?
如图,已知GP平分∠EGB,HQ平分∠GHD,如果∠1=∠2,那么GP∥HQ吗?为什么? 如图,∠ABC=∠ACB.∠ABC、∠ACB的平分线分别交AC、AB于点D、E,且∠1=∠2,试说明CE∥DF.
如图,∠ABC=∠ACB.∠ABC、∠ACB的平分线分别交AC、AB于点D、E,且∠1=∠2,试说明CE∥DF.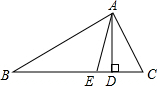 如图,在△ABC中,AD是高,AE是角平分线,∠B=28°,∠C=60°,则∠DAE=16°.
如图,在△ABC中,AD是高,AE是角平分线,∠B=28°,∠C=60°,则∠DAE=16°.