题目内容
16.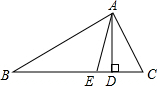 如图,在△ABC中,AD是高,AE是角平分线,∠B=28°,∠C=60°,则∠DAE=16°.
如图,在△ABC中,AD是高,AE是角平分线,∠B=28°,∠C=60°,则∠DAE=16°.
分析 根据三角形的内角和定理求出∠BAC,再根据角平分线的定义求出∠CAE,根据直角三角形两锐角互余求出∠DAC,然后根据∠DAE=∠EAC-∠DAC代入数据计算即可得解.
解答 解:在△ABC中,∵∠B=28°,∠C=60°,
∴∠BAC=180°-∠B-∠C=180°-28°-60°=92°,
∵AE是的角平分线,
∴∠EAC=$\frac{1}{2}$∠BAC=46°,
∵AD是高,
∴∠ADC=90°,
∴在△ADC中,∠DAC=180°-∠ADC-∠C=180°-90°-60°=30°,
∴∠DAE=∠EAC-∠DAC=46°-30°=16°.
故答案为16.
点评 本题考查了三角形的内角和定理,角平分线的定义,直角三角形两锐角互余的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
9.由方程组$\left\{\begin{array}{l}x+2y=4-m\\ x-y=m\end{array}\right.$可得出x与y之间的关系是( )
| A. | 2x+y=4 | B. | 2x+y=4m | C. | 2x+y=-4 | D. | 2x+y=-4m |
8.下列实数中,是无理数的为( )
| A. | $\frac{2}{3}$ | B. | 0 | C. | $\sqrt{36}$ | D. | -π |
5.若sin(α-10o)=$\frac{{\sqrt{3}}}{2}$,则∠α为( )
| A. | 30° | B. | 40° | C. | 60° | D. | 70° |