题目内容
2. 如图,∠ABC=∠ACB.∠ABC、∠ACB的平分线分别交AC、AB于点D、E,且∠1=∠2,试说明CE∥DF.
如图,∠ABC=∠ACB.∠ABC、∠ACB的平分线分别交AC、AB于点D、E,且∠1=∠2,试说明CE∥DF.
分析 先根据等腰三角形的性质以及角平分线的定义,得出∠1=∠3,再根据∠1=∠2,即可得到∠2=∠3,进而得到CE∥DF.
解答  证明:∵∠ABC=∠ACB,∠ABC、∠ACB的平分线分别为BD,CE,
证明:∵∠ABC=∠ACB,∠ABC、∠ACB的平分线分别为BD,CE,
∴∠1=$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ACB=∠3,
又∵∠1=∠2,
∴∠2=∠3,
∴CE∥DF.
点评 本题主要考查了等腰三角形的性质,平行线的判定以及角平分线的定义的运用,解题时注意:内错角相等,两直线平行.

练习册系列答案
相关题目
8.下列实数中,是无理数的为( )
| A. | $\frac{2}{3}$ | B. | 0 | C. | $\sqrt{36}$ | D. | -π |
 如图,在△ABC中,∠ACB=90°,AC=4,BC=3,点D在边BC上,BD=5CD,DE⊥AB,垂足为E.
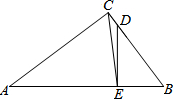
如图,在△ABC中,∠ACB=90°,AC=4,BC=3,点D在边BC上,BD=5CD,DE⊥AB,垂足为E. 如图,在四边形ACDB中,AC=CD,∠ACD=∠ABD=90°,∠BCD=30°,BD=$\sqrt{2}$,求BC的长.
如图,在四边形ACDB中,AC=CD,∠ACD=∠ABD=90°,∠BCD=30°,BD=$\sqrt{2}$,求BC的长.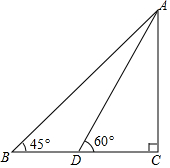 如图,某滑雪运动员训练时的斜坡示意图,某次训练拟将难度系数加大,决定将训练的斜坡的倾角由45°升为60°,已知原斜坡AB的长为3$\sqrt{6}$米,点B、D、C在同一水平地面上.若斜坡的正前方能有6米长的空地就能保证安全,已知原斜坡屈的前方有3米长的空地,进行这样的改造是否可行?并说明理由.(参考数据:$\sqrt{3}$=1.732,$\sqrt{6}$=2.449)
如图,某滑雪运动员训练时的斜坡示意图,某次训练拟将难度系数加大,决定将训练的斜坡的倾角由45°升为60°,已知原斜坡AB的长为3$\sqrt{6}$米,点B、D、C在同一水平地面上.若斜坡的正前方能有6米长的空地就能保证安全,已知原斜坡屈的前方有3米长的空地,进行这样的改造是否可行?并说明理由.(参考数据:$\sqrt{3}$=1.732,$\sqrt{6}$=2.449)