题目内容
 如图,在平面直角坐标中,矩形OABC的顶点O为坐标原点,OA在x轴上,OC在y轴上,点B的坐标为(-3,4),反比例函数y=
如图,在平面直角坐标中,矩形OABC的顶点O为坐标原点,OA在x轴上,OC在y轴上,点B的坐标为(-3,4),反比例函数y=| k |
| x |
考点:反比例函数综合题
专题:
分析:首先求得直线AC的解析式.设B′(x、
x+4).作出折叠后的草图,根据反比例函数解析式表示出点E、F的坐标,过点B′作B′H⊥BC于点H,B′G⊥AB于点G,可得△GEB′∽△HFB′,根据相似三角形的对应边成比例列式整理,求得点B′的坐标,然后在直角△GEB′中由勾股定理来求k的值.
| 4 |
| 3 |
解答: 解:如图,∵在平面直角坐标系中,矩形OABC的顶点O为坐标原点,OA在x轴上,OC在y轴上,点B的坐标为(-3,4),
解:如图,∵在平面直角坐标系中,矩形OABC的顶点O为坐标原点,OA在x轴上,OC在y轴上,点B的坐标为(-3,4),
∴A(-3,0),C(0,4).
∴直线AC为:y=
x+4.
故设B′(x,
x+4).
∵点E、F在双曲线y=
(k≠O)上,
∴设E(-3,-
),F(
,4).
根据折叠的性质知△EBF≌△EB′F,则BF=B′F,BE=B′E,∠EBF=∠EB′F=90°.
如图,过点B′作B′H⊥BC于点H,B′G⊥AB于点G,则∠EB′G=∠FB′H,∠EGB′=∠FHB′,
∴GEB′∽△HFB′,
∴
=
,即
=
,
整理得-
=
,
解得 x=-
.
则B′(-
,
).
∴GE=
+
,B′G=3-
=
.
∴在直角△GEB′中,由勾股定理,得
B′E2=GE2+B′G2,即(4+
)2=(
+
)2+(
)2,
解得 k=-6.
∴反比例函数的解析式为 y=-
.
故答案是:y=-
.
 解:如图,∵在平面直角坐标系中,矩形OABC的顶点O为坐标原点,OA在x轴上,OC在y轴上,点B的坐标为(-3,4),
解:如图,∵在平面直角坐标系中,矩形OABC的顶点O为坐标原点,OA在x轴上,OC在y轴上,点B的坐标为(-3,4),∴A(-3,0),C(0,4).
∴直线AC为:y=
| 4 |
| 3 |
故设B′(x,
| 4 |
| 3 |
∵点E、F在双曲线y=
| k |
| x |
∴设E(-3,-
| k |
| 3 |
| k |
| 4 |
根据折叠的性质知△EBF≌△EB′F,则BF=B′F,BE=B′E,∠EBF=∠EB′F=90°.
如图,过点B′作B′H⊥BC于点H,B′G⊥AB于点G,则∠EB′G=∠FB′H,∠EGB′=∠FHB′,
∴GEB′∽△HFB′,
∴
| GB′ |
| HB′ |
| EB′ |
| FB′ |
| |-3-x| | ||
|4-
|
4+
| ||
3+
|
整理得-
| 9+3x |
| 4x |
| 4 |
| 3 |
解得 x=-
| 27 |
| 25 |
则B′(-
| 27 |
| 25 |
| 64 |
| 25 |
∴GE=
| 64 |
| 25 |
| k |
| 3 |
| 27 |
| 25 |
| 48 |
| 25 |
∴在直角△GEB′中,由勾股定理,得
B′E2=GE2+B′G2,即(4+
| k |
| 3 |
| 64 |
| 25 |
| k |
| 3 |
| 48 |
| 25 |
解得 k=-6.
∴反比例函数的解析式为 y=-
| 6 |
| x |
故答案是:y=-
| 6 |
| x |
点评:本题综合考查了矩形的性质、相似三角形的判定与性质、勾股定理、折叠的性质应用以及反比例函数综合题.此题的难度较大,希望同学们在解题时要开动脑筋,从多方位全面的考虑问题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 把长方形AB′CD沿对角线AC折叠,得到如图所示的三角形.已知∠BAO=30°,求∠AOC和∠BAC的度数.
把长方形AB′CD沿对角线AC折叠,得到如图所示的三角形.已知∠BAO=30°,求∠AOC和∠BAC的度数.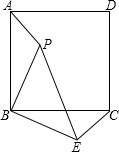 已知:点P是正方形内一点,△ABP旋转后能与△CBE重合.
已知:点P是正方形内一点,△ABP旋转后能与△CBE重合. 如图,△ABC中,∠B,∠C的平分线相交于点O,过O作DE∥BC,若BD+EC=5,则DE等于多少?
如图,△ABC中,∠B,∠C的平分线相交于点O,过O作DE∥BC,若BD+EC=5,则DE等于多少? 如图,△ABC为等腰三角形,AB=AC,BD为角平分线,延长BC到E,使CE=CD,作DH⊥BE,垂足为H.
如图,△ABC为等腰三角形,AB=AC,BD为角平分线,延长BC到E,使CE=CD,作DH⊥BE,垂足为H.