题目内容
已知关于x的一元二次方程(c-b)x2+a-b=2(b-a)x有两个相等的实数根,求证:以a,b,c为边组成的三角形是等腰三角形.
考点:根的判别式,等腰三角形的判定
专题:证明题
分析:若一元二次方程有两个相等的实数根,则根的判别式△=b2-4ac=0,即[-2(b-a)]2-4(c-b)(a-b)=0,再利用完全平方公式得出即可.
解答:解:∵关于x的一元二次方程(c-b)x2+a-b=2(b-a)x有两个相等的实数根,
∴(c-b)x2-2(b-a)x+(a-b)=0
∴△=[-2(b-a)])2-4(c-b)(a-b)=0,
∴(a-b)2-(c-b)(a-b)=0,
∴(a-b)[(a-b)-(c-b)]=0,
∴a-b=0或a-b-(c-b)=0,
∴a=b或a=c,
即以a,b,c为边组成的三角形是等腰三角形.
∴(c-b)x2-2(b-a)x+(a-b)=0
∴△=[-2(b-a)])2-4(c-b)(a-b)=0,
∴(a-b)2-(c-b)(a-b)=0,
∴(a-b)[(a-b)-(c-b)]=0,
∴a-b=0或a-b-(c-b)=0,
∴a=b或a=c,
即以a,b,c为边组成的三角形是等腰三角形.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
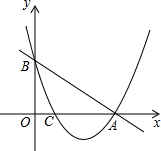 如图,直线y=-x+3交x轴于点A,交y轴于点B,抛物线经过A、B、C三点.点C的坐标为(1,0).
如图,直线y=-x+3交x轴于点A,交y轴于点B,抛物线经过A、B、C三点.点C的坐标为(1,0). 画出如图所示的物体满足下列条件的正投影.
画出如图所示的物体满足下列条件的正投影. 在平面直角坐标系中,如图,将线段AB平移至线段CD,连接AC、BD.
在平面直角坐标系中,如图,将线段AB平移至线段CD,连接AC、BD.  如图,在等腰△ABC中,AB=BC=8cm,动点P从A点出发,沿AB向B移动.过点P作平行于BC、AC的直线,分别与AC、BC交于点R、Q.当动点P从A点出发移动多少厘米时,?PQCR的面积等于16cm2?
如图,在等腰△ABC中,AB=BC=8cm,动点P从A点出发,沿AB向B移动.过点P作平行于BC、AC的直线,分别与AC、BC交于点R、Q.当动点P从A点出发移动多少厘米时,?PQCR的面积等于16cm2?