题目内容
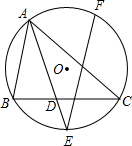 如图,圆的内接△ABC中,∠BAC的平分线AD的延长线交⊙O于点E,过点E作弦EF,使EF=AC,求证:EF∥AB.
如图,圆的内接△ABC中,∠BAC的平分线AD的延长线交⊙O于点E,过点E作弦EF,使EF=AC,求证:EF∥AB.考点:圆心角、弧、弦的关系,圆周角定理
专题:证明题
分析:先根据圆心角、弧、弦的关系由EF=AC得到
=
,则
=
,再根据圆周角定理得∠E=∠EAC,由于∠BAE=∠EAC,所以∠E=∠BAE,然后根据平行线的判定即可得到EF∥AB.
 |
| EF |
 |
| AC |
 |
| AF |
 |
| CE |
解答:证明:∵EF=AC,
∴
=
,即
+
=
+
,
∴
=
,
∴∠E=∠EAC,
∵AE平分∠BAC,
∴∠BAE=∠EAC,
∴∠E=∠BAE,
∴EF∥AB.
∴
 |
| EF |
 |
| AC |
 |
| AF |
 |
| CF |
 |
| CF |
 |
| CE |
∴
 |
| AF |
 |
| CE |
∴∠E=∠EAC,
∵AE平分∠BAC,
∴∠BAE=∠EAC,
∴∠E=∠BAE,
∴EF∥AB.
点评:本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了圆周角定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,以A、B、C、D、O作为线段的端点,共有线段( )
如图,以A、B、C、D、O作为线段的端点,共有线段( )| A、6条 | B、8条 |
| C、10条 | D、12条 |
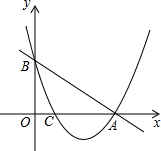 如图,直线y=-x+3交x轴于点A,交y轴于点B,抛物线经过A、B、C三点.点C的坐标为(1,0).
如图,直线y=-x+3交x轴于点A,交y轴于点B,抛物线经过A、B、C三点.点C的坐标为(1,0). 在平面直角坐标系中,如图,将线段AB平移至线段CD,连接AC、BD.
在平面直角坐标系中,如图,将线段AB平移至线段CD,连接AC、BD.