Question

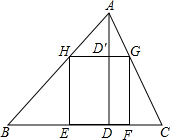在一底为8米，高为6米的三角形钢板上剪一个面积最大的矩形．
（1）写出矩形的长GH=x与矩形面积S的函数关系式．
（2）求出矩形的最大面积．

Answer 1

考点：相似三角形的应用,二次函数的最值

专题：

分析：（1）首先根据平行线得到相似三角形，然后用x表示出矩形的一边长，然后利用矩形的面积计算方法列出函数关系式即可；
（2）将二次函数配方后即可确定二次函数的最大值．

解答：解：∵四边形HEFG是矩形，
∴HG∥BC，
∴△AHG∽△ABC，
∴

AD′

AD

=

HG

BC

，
即：

AD′

6

=

x

8

，
解得：AD′=

3

4

x，
∴DD′=（6-

3

4

x），
∴S=HG•EF=x（6-

3

4

x）=-

3

4

x²+6x；

（2）∵S=-

3

4

x²+6x=-

3

4

（x-4）²+12，
∴最大面积为12平方米．

点评：本题考查了相似三角形的应用及二次函数的最值，解题的关键是能够表示出矩形的一边长，难度不大．