Question

11．请画出二次函数y=x²-5x+4的简图，问当x取何值时，（1）y＞0；（2）y=0；（3）y＜0？

Answer 1

分析 解方程求出抛物线与x轴的交点，画出简图，结合图象解答即可．

解答 解：x²-5x+4=0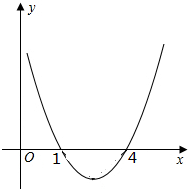
（x-1）（x-4）=0
x₁=1，x₂=4，
则抛物线y=x²-5x+4与x轴的交点坐标为：（1，0），（4，0），
简图如图所示：
由图象可知：
（1）当x＜1或x＞4时，y＞0；
（2）当x=1或x=4时，y=0；
（3）当1＜x＜4时，y＜0．

点评 本题考查的是抛物线与x轴的交点，求二次函数y=ax²+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标，令y=0，即ax²+bx+c=0，解关于x的一元二次方程即可求得交点横坐标．解答时，注意数形结合思想的灵活运用．