题目内容
2.近些年全国各地频发雾霾天气,给人民群众的身体健康带来了危害,某商场看到商机后,决定购进空气净化器进行销售,现有甲、乙两种空气净化器可供选择.(1)若每台甲种空气净化器的进价比每台乙种空气净化器的进价少300元,且用6000元购进甲种空气净化器的数量与用7500元购进乙种空气净化器的数量相同.求每台甲种空气净化器、每台乙种空气净化器的进价分别为多少元?
(2)在(1)的条件下,该商场准备用18000元来购买甲、乙两种空气净化器中的一种,已知该商场在出售空气净化器时,每台甲种空气净化器的售价为1400元,每台乙种空气净化器的售价为1800元,该商场选用哪种空气净化器能获得更大利润?
分析 (1)设每台甲种空气净化器为x元,乙种净化器为(x+300)元,根据用6000元购进甲种空气净化器的数量与用7500元购进乙种空气净化器的数量相同,列方程求解;
(2)分别求出甲种空气净化器的利润,乙种空气净化器的利润为,再比较即可.
解答 解:设每台甲种空气净化器为x元,乙种净化器为(x+300)元,
由题意得,$\frac{6000}{x}$=$\frac{7500}{x+300}$,
解得:x=1200,
经检验x=1200是原方程的解,
则x+300=1500(元),
答:每台甲种空气净化器、每台乙种空气净化器的进价分别为1200元,1500元;
(2)∵甲种空气净化器的利润为:$\frac{18000}{1200}$×(1400-1200)=3000元,
乙种空气净化器的利润为:$\frac{18000}{1500}$×(1800-1500)=3600元,
∴该商场选用乙种空气净化器能获得更大利润.
点评 本题考查了分式方程的应用,解答本题的关键是读懂题意,找出合适的等量关系,列方程求解.

练习册系列答案
相关题目
7.若关于x的方程$\frac{3}{x-3}$=$\frac{2}{k-3}$有正根,则k的取值范围是( )
| A. | k>1 | B. | k>3 | C. | k≠3 | D. | k>1且k≠3 |
14.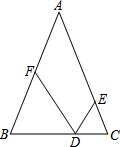 如图,在△ABC中,AB=AC,∠A=40°,CE=CD,BD=BF,则∠EDF的度数为( )
如图,在△ABC中,AB=AC,∠A=40°,CE=CD,BD=BF,则∠EDF的度数为( )
 如图,在△ABC中,AB=AC,∠A=40°,CE=CD,BD=BF,则∠EDF的度数为( )
如图,在△ABC中,AB=AC,∠A=40°,CE=CD,BD=BF,则∠EDF的度数为( )| A. | 40° | B. | 55° | C. | 65° | D. | 70° |
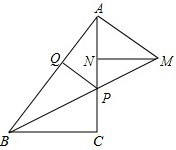 如图,已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN,NP=2,PC=3.
如图,已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN,NP=2,PC=3. 如图,已知四边形ABCD,其中A(1,1),B(2,2),C(0,3),D(-3,0),作出四边形ABCD关于原点对称的四边形A′B′C′D′.
如图,已知四边形ABCD,其中A(1,1),B(2,2),C(0,3),D(-3,0),作出四边形ABCD关于原点对称的四边形A′B′C′D′.