题目内容
6.二次函数y=x2-2x-3的图象与x轴有公共点吗?如果有,求出公共点的坐标.分析 根据△=b2-4ac>0时,抛物线与x轴有2个交点判断图象与x轴是否有公共点,解一元二次方程求出交点坐标.
解答 解:△=(-2)2-4×1×(-3)=16>0,
则图象与x轴有公共点,
x2-2x-3=0,
x1=-1,x2=3,
则图象与x轴的公共点的坐标为:(-1,0)和(3,0).
点评 本题考查的是抛物线与x轴的交点.△=b2-4ac决定抛物线与x轴的交点个数.△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
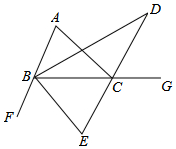 如图,∠CBF、∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC、∠CBF的平分线BD、BE交于点D、E.
如图,∠CBF、∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC、∠CBF的平分线BD、BE交于点D、E.

 如图,已知四边形ABCD,其中A(1,1),B(2,2),C(0,3),D(-3,0),作出四边形ABCD关于原点对称的四边形A′B′C′D′.
如图,已知四边形ABCD,其中A(1,1),B(2,2),C(0,3),D(-3,0),作出四边形ABCD关于原点对称的四边形A′B′C′D′.