题目内容
20.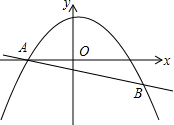 如图,抛物线${y_1}=-\frac{1}{4}{x^2}+\frac{1}{4}x+3$与直线${y_2}=-\frac{1}{4}x-\frac{3}{4}$交于A、B两点,则使y1≥y2成立的x取值范围是-2≤x≤5.
如图,抛物线${y_1}=-\frac{1}{4}{x^2}+\frac{1}{4}x+3$与直线${y_2}=-\frac{1}{4}x-\frac{3}{4}$交于A、B两点,则使y1≥y2成立的x取值范围是-2≤x≤5.
分析 首先解方程求得两个函数交点的横坐标,根据图象使y1≥y2成立的x取值范围是:能使y1在上方的部分自变量的取值范围.
解答 解:根据题意得:-$\frac{1}{4}$x2+$\frac{1}{4}$x+3=-$\frac{1}{4}$x-$\frac{3}{4}$,
即x2-2x-15=0,
解得:x1=-2,x2=5.
则A和B的横坐标分别是-2和5.
故使y1≥y2成立的x取值范围是:-2≤x≤5.
故答案是:-2≤x≤5.
点评 本题考查了二次函数与不等式,利用两个函数图象在直角坐标系中的上下位置关系求自变量的取值范围,利用交点直观求解.

练习册系列答案
相关题目
8.某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:km)
(1)求收工时,检修小组在A地的哪个方向?距离A地多远?
(2)在第几次纪录时距A地最远?
(3)若汽车行驶每千米耗油0.2升,问从A地出发,检修结束后再回到A地共耗油多少升?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -4 | +7 | -9 | +8 | +6 | -5 | -4 |
(2)在第几次纪录时距A地最远?
(3)若汽车行驶每千米耗油0.2升,问从A地出发,检修结束后再回到A地共耗油多少升?
10.若关于x的一元二次方程kx2-6x+3=0有两个实数根,则k的取值范围中,非负整数值有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
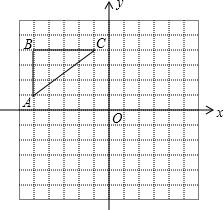 如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题:
如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题: 如图,△ABC中,BC=10,DH为AB的中垂线,EF垂直平分AC,则△ADE的周长是10.
如图,△ABC中,BC=10,DH为AB的中垂线,EF垂直平分AC,则△ADE的周长是10.