题目内容
2.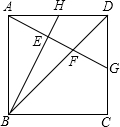 如图,正方形ABCD,H为AD中点,AG⊥BH分别交BH、BD、CD于E、F、G.
如图,正方形ABCD,H为AD中点,AG⊥BH分别交BH、BD、CD于E、F、G.(1)求证:△ABH≌△DAG;
(2)若AB=2,求EF的长.
分析 (1)根据两角夹边相等的两个三角形全等即可判断.
(2)由DG∥AB,得到$\frac{DG}{AB}=\frac{FG}{AF}$=$\frac{1}{2}$求出AF,再根据面积法求出AE,利用EF=AF-AE即可解决问题.
解答  (1)证明:∵四边形ABCD是正方形,
(1)证明:∵四边形ABCD是正方形,
∴AB=AD=DC=BC,∠BAC=∠ADC=90°,
∵AG⊥BH,
∴∠ABH+∠BAE=90°,∠BAE+∠DAG=90°,
∴∠ABH=∠DAG,
在△ABH和△DAG中,
$\left\{\begin{array}{l}{∠BAH=∠ADC}\\{AB=AD}\\{∠ABH=∠DAG}\end{array}\right.$,
∴△ABH≌△DAG.
(2)∵AB=AD=CD=2,AH=DH=1,
又∵△ABH≌△DAG,
∴AH=DG=1,BH=AG=$\sqrt{A{B}^{2}+A{H}^{2}}$=$\sqrt{5}$,
∵DG∥AB,
∴$\frac{DG}{AB}$=$\frac{FG}{AF}$=$\frac{1}{2}$,
∴AF=$\frac{2}{3}$AG=$\frac{2\sqrt{5}}{3}$,
∵$\frac{1}{2}$•BH•AE=$\frac{1}{2}$•AB•AH,
∴AH=$\frac{2\sqrt{5}}{5}$,
∴EF=AF-AE=$\frac{2\sqrt{5}}{3}$-$\frac{2\sqrt{5}}{5}$=$\frac{4\sqrt{5}}{15}$.
点评 本题考查正方形的性质、全等三角形的判断和性质、平行线分线段成比例定理、勾股定理等知识,解题的关键是正确寻找全等三角形,利用平行成比例解问题,学会用面积法求直角三角形斜边上的高,属于中考常考题型.

 应用题作业本系列答案
应用题作业本系列答案 某班开展安全知识竞赛活动,满分为100分,得分为整数,全班同学的成绩都在60分以上.班长将所有同学的成绩分成四组,并制作了所示的统计图表:
某班开展安全知识竞赛活动,满分为100分,得分为整数,全班同学的成绩都在60分以上.班长将所有同学的成绩分成四组,并制作了所示的统计图表:| 类别 | 成绩 | 频数 |
| 甲 | 60≤m<70 | 5 |
| 乙 | 70≤m<80 | a |
| 丙 | 80≤m<90 | 10 |
| 丁 | 90≤m≤100 | 5 |
(1)该班共有学生40人;表中a=20;
(2)丁组的五名学生中有2名女生,3名男生,现从丁组中随机挑选两名学生参加学校的决赛,请借助树状图、列表或列举等方式,求参加决赛的两名学生是一男、一女的概率.
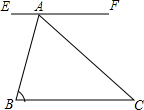 如图,EF∥BC,AC平分∠BAF,∠B=70°,则∠C的度数是( )
如图,EF∥BC,AC平分∠BAF,∠B=70°,则∠C的度数是( )| A. | 70° | B. | 60° | C. | 55° | D. | 50° |
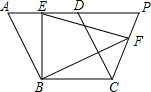 如图,在平行四边形ABCD,BE⊥AD于点E,且点E为AD中点,tanA=2,点P在AD的延长线上,作EF⊥CP于点F,连接BF.
如图,在平行四边形ABCD,BE⊥AD于点E,且点E为AD中点,tanA=2,点P在AD的延长线上,作EF⊥CP于点F,连接BF.