题目内容
4. 如图,直线l1∥l2,∠A=124°,∠B=86°,则∠1+∠2=( )
如图,直线l1∥l2,∠A=124°,∠B=86°,则∠1+∠2=( )| A. | 30° | B. | 35° | C. | 36° | D. | 40° |
分析 过点A作AC∥l1,过点B作BD∥l1,根据平行公理可得l1∥AC∥BD∥l2,根据两直线平行,内错角相等可得∠3=∠1,∠4=∠2,再根据两直线平行,同旁内角互补可得∠CAB+∠ABD=180°,然后求出∠3+∠4,再求解即可.
解答  解:如图,过点A作AC∥l1,过点B作BD∥l1,
解:如图,过点A作AC∥l1,过点B作BD∥l1,
∵直线l1∥l2,
∴l1∥AC∥BD∥l2,
∴∠3=∠1,∠4=∠2,
∠CAB+∠ABD=180°,
∴∠3+∠4=124°+86°-180°=30°,
∴∠1+∠2=∠3+∠4=30°.
故选A.
点评 本题考查了平行线的性质,此类题目,过拐点作平行线是解题的关键,本题要注意整体思想的利用.

练习册系列答案
相关题目

 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.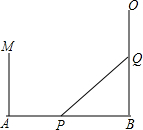 如图,已知AB=20米,MA⊥AB于A,MA=10米,射线BD⊥AB于B,P点从B点向A运动,每秒走2米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发4秒后,在线段MA上有一点C,使△CAP与△PBQ全等.
如图,已知AB=20米,MA⊥AB于A,MA=10米,射线BD⊥AB于B,P点从B点向A运动,每秒走2米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发4秒后,在线段MA上有一点C,使△CAP与△PBQ全等.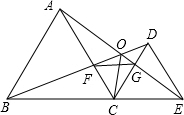 如图所示,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④OE=OD+OC.其中正确结论的个数 ( )
如图所示,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④OE=OD+OC.其中正确结论的个数 ( )