题目内容
方程|x+1|-2|x-2|=1的解为 .
考点:含绝对值符号的一元一次方程
专题:
分析:分类讨论:x<-1,-1≤x<2,x≥2,根据绝对值的意义,可化简方程,根据解方程,可得答案.
解答:解:当x<-1时,原方程等价于x-5=1,解得x=4(不符合题意要舍去);
当-1≤x<2时,原方程等价于3x-3=1,解得x=
;
当x≥2时,原方程等价于-x+5=1,解得x=4;
综上所述:x=
或x=4.
故答案为:x=
或x=4.
当-1≤x<2时,原方程等价于3x-3=1,解得x=
| 4 |
| 3 |
当x≥2时,原方程等价于-x+5=1,解得x=4;
综上所述:x=
| 4 |
| 3 |
故答案为:x=
| 4 |
| 3 |
点评:本题考查了含绝对值符号的一元一次方程,分类讨论是解题关键.

练习册系列答案
相关题目
 如图,BD平分∠ABC,AD⊥BD于D,CE平分∠ACB的外角,AE⊥CE于E,AC=6,BC=9,AB=7,则DE的长是
如图,BD平分∠ABC,AD⊥BD于D,CE平分∠ACB的外角,AE⊥CE于E,AC=6,BC=9,AB=7,则DE的长是 如图,直线AB分别交x轴,y轴于点A,B,
如图,直线AB分别交x轴,y轴于点A,B, 如图,平行四边形ABCD中,AC⊥AB,AC与BD相交于O,OC=1,CD=
如图,平行四边形ABCD中,AC⊥AB,AC与BD相交于O,OC=1,CD= 如图,已知∠1=∠2,DE⊥AB于点E,CF⊥AB于点F,请你判断FG与BC是否平行,并说明理由.
如图,已知∠1=∠2,DE⊥AB于点E,CF⊥AB于点F,请你判断FG与BC是否平行,并说明理由.

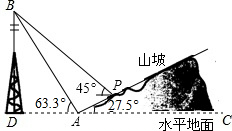 如图,某人在山脚A处测得一座塔BD的塔尖点B的仰角为63.3°,沿山坡向上走到P处再测得点B的仰角为45°,已知坡面AP=40米,坡角∠PAC=27.5°,且D、A、C在同一条直线上,求塔BD的高度(结果精确到1m)(参考数据:tan63.3°≈1.99,sin63.3°≈0.89,cos63.3°≈0.45,cos27.5°≈0.89,tan27.5°≈0.52,sin27.5°≈0.46)
如图,某人在山脚A处测得一座塔BD的塔尖点B的仰角为63.3°,沿山坡向上走到P处再测得点B的仰角为45°,已知坡面AP=40米,坡角∠PAC=27.5°,且D、A、C在同一条直线上,求塔BD的高度(结果精确到1m)(参考数据:tan63.3°≈1.99,sin63.3°≈0.89,cos63.3°≈0.45,cos27.5°≈0.89,tan27.5°≈0.52,sin27.5°≈0.46)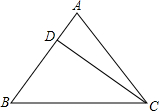 已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,
已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,