题目内容
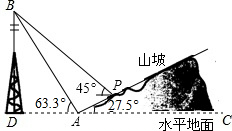 如图,某人在山脚A处测得一座塔BD的塔尖点B的仰角为63.3°,沿山坡向上走到P处再测得点B的仰角为45°,已知坡面AP=40米,坡角∠PAC=27.5°,且D、A、C在同一条直线上,求塔BD的高度(结果精确到1m)(参考数据:tan63.3°≈1.99,sin63.3°≈0.89,cos63.3°≈0.45,cos27.5°≈0.89,tan27.5°≈0.52,sin27.5°≈0.46)
如图,某人在山脚A处测得一座塔BD的塔尖点B的仰角为63.3°,沿山坡向上走到P处再测得点B的仰角为45°,已知坡面AP=40米,坡角∠PAC=27.5°,且D、A、C在同一条直线上,求塔BD的高度(结果精确到1m)(参考数据:tan63.3°≈1.99,sin63.3°≈0.89,cos63.3°≈0.45,cos27.5°≈0.89,tan27.5°≈0.52,sin27.5°≈0.46)考点:解直角三角形的应用-仰角俯角问题
专题:
分析:过P点作PE⊥AC于E点,PF⊥BD于F点,设BD=x,则AD=AD=
,根据DE=PF=BF=BD-FD,DE=AD+AE,列出方程,求出x的值即可.
| x |
| tan63.3° |
解答: 解:过P点作PE⊥AC于E点,PF⊥BD于F点,
解:过P点作PE⊥AC于E点,PF⊥BD于F点,
在Rt△APE中,∵AP=40,∠PAC=27.5°,
∴PE=40sin27.5°=20.8,AE=40cos27.5°=35.6,
设BD=x,则AD=
≈0.5x,
∵DE=PF=BF=BD-FD,DE=AD+AE,
∴0.5x+35.6=x-20.8,
解得:x=112.8.
∴塔BD的高度为112.8米.
 解:过P点作PE⊥AC于E点,PF⊥BD于F点,
解:过P点作PE⊥AC于E点,PF⊥BD于F点,在Rt△APE中,∵AP=40,∠PAC=27.5°,
∴PE=40sin27.5°=20.8,AE=40cos27.5°=35.6,
设BD=x,则AD=
| x |
| tan63.3° |
∵DE=PF=BF=BD-FD,DE=AD+AE,
∴0.5x+35.6=x-20.8,
解得:x=112.8.
∴塔BD的高度为112.8米.
点评:本题考查了解直角三角形的应用-仰角俯角问题以及坡度坡角问题,本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
 如图,AC平分∠BCD,且∠BCA=∠CAD=
如图,AC平分∠BCD,且∠BCA=∠CAD=| 1 |
| 2 |
| A、36° | B、35° |
| C、37.5° | D、70° |
 如图是一圆锥的侧面展开图,其弧长为10π,则该圆锥的全面积为 ( )
如图是一圆锥的侧面展开图,其弧长为10π,则该圆锥的全面积为 ( )| A、60π | B、85π |
| C、95π | D、169π |
 一根12米的电线杆AB,用铁丝AC、AD固定,现已知用去铁丝AC=15米,AD=13米,又测得地面上B、C两点之间距离是9米,B、D两点之间距离是5米,则电线杆和地面是否垂直,为什么?
一根12米的电线杆AB,用铁丝AC、AD固定,现已知用去铁丝AC=15米,AD=13米,又测得地面上B、C两点之间距离是9米,B、D两点之间距离是5米,则电线杆和地面是否垂直,为什么?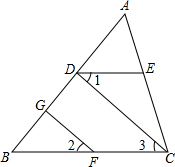 如图所示,已知∠ADE=∠B,∠1=∠2,GF⊥AB,求证:CD⊥AB.
如图所示,已知∠ADE=∠B,∠1=∠2,GF⊥AB,求证:CD⊥AB. 如图,在?ABCD中,E,F在AC边上,G,H在BD边上,且AE=CF,BH=DG,求证:EG∥HF.
如图,在?ABCD中,E,F在AC边上,G,H在BD边上,且AE=CF,BH=DG,求证:EG∥HF.