题目内容
 如图,BD平分∠ABC,AD⊥BD于D,CE平分∠ACB的外角,AE⊥CE于E,AC=6,BC=9,AB=7,则DE的长是
如图,BD平分∠ABC,AD⊥BD于D,CE平分∠ACB的外角,AE⊥CE于E,AC=6,BC=9,AB=7,则DE的长是考点:三角形中位线定理,等腰三角形的判定与性质
专题:
分析:延长AD、AE分别角BC与BC的延长线于M、N,根据等腰三角形三线合一的性质可得AD=MD,AB=MB,AE=EN,AC=CN,再求出MN,并判断出DE是△AMN的中位线,然后根据三角形的中位线平行于第三边并且等于第三边的一半可得DE=
MN.
| 1 |
| 2 |
解答: 解:如图,延长AD、AE分别角BC与BC的延长线于M、N,
解:如图,延长AD、AE分别角BC与BC的延长线于M、N,
∵BD平分∠ABC,AD⊥BD于D,
∴AD=MD,AB=MB=7,
∵CE平分∠ACB的外角,AE⊥CE于E,
∴AE=EN,AC=CN=6,
∴DE是△AMN的中位线,
∵BC=9,
∴MN=CN+BC-BM=6+9-7=8,
∴DE=
MN=
×8=4.
故答案为:4.
 解:如图,延长AD、AE分别角BC与BC的延长线于M、N,
解:如图,延长AD、AE分别角BC与BC的延长线于M、N,∵BD平分∠ABC,AD⊥BD于D,
∴AD=MD,AB=MB=7,
∵CE平分∠ACB的外角,AE⊥CE于E,
∴AE=EN,AC=CN=6,
∴DE是△AMN的中位线,
∵BC=9,
∴MN=CN+BC-BM=6+9-7=8,
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:4.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等腰三角形的判定与性质,熟记性质与定理并作辅助线构造出以DE为中位线的三角形是解题的关键.

练习册系列答案
相关题目
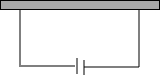 如图,要建一个面积为130m2的养鸡场,鸡场的一边靠墙(墙长16m),并在与墙平行一边开一道1m宽的门,现有32m长的木板.
如图,要建一个面积为130m2的养鸡场,鸡场的一边靠墙(墙长16m),并在与墙平行一边开一道1m宽的门,现有32m长的木板.
 一个物体的主视图如图所示,请你画出这个物体的俯视图(要求分别画出三种不同的情形)
一个物体的主视图如图所示,请你画出这个物体的俯视图(要求分别画出三种不同的情形) 一根12米的电线杆AB,用铁丝AC、AD固定,现已知用去铁丝AC=15米,AD=13米,又测得地面上B、C两点之间距离是9米,B、D两点之间距离是5米,则电线杆和地面是否垂直,为什么?
一根12米的电线杆AB,用铁丝AC、AD固定,现已知用去铁丝AC=15米,AD=13米,又测得地面上B、C两点之间距离是9米,B、D两点之间距离是5米,则电线杆和地面是否垂直,为什么? 如图所示,点D在直线AB上,∠ADE=∠ABC,且DG,BF分别是∠ADE和∠ABC的平分线,那么DG一定平行于BF,为什么?
如图所示,点D在直线AB上,∠ADE=∠ABC,且DG,BF分别是∠ADE和∠ABC的平分线,那么DG一定平行于BF,为什么?