题目内容
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴A、B两点之间的距离AB=|a-b|.例如:数轴上表示2和8两点间的距离|2-8|=6,数轴上表示-3和4两点的距离等于|-3-4|=7,利用上述知识回答如下问题:

(1)数轴上表示1和5两点之间的距离是 ,数轴上表示2和-1的两点之间的距离是 ;
(2)数轴上表示x和-1的两点之间的距离表示为 ;
(3)若x表示一个有理数,且-4<x<2,则|x-2|+|x+4|= .
(4)利用数轴求出|x+3|+|x-4|的最小值,并写出此时x可取哪些整数值?


(1)数轴上表示1和5两点之间的距离是
(2)数轴上表示x和-1的两点之间的距离表示为
(3)若x表示一个有理数,且-4<x<2,则|x-2|+|x+4|=
(4)利用数轴求出|x+3|+|x-4|的最小值,并写出此时x可取哪些整数值?

考点:绝对值,数轴
专题:
分析:(1)根据已知中的A、B两点之间的距离AB=|a-b|.即可得到答案;
(2)把x与-1代入|a-b|即可得到答案;
(3)当-4<x<2时,根据绝对值的性质,即可化简|x-2|+|x+4|得到答案;
(4)求|x+3|+|x-4|的最小值,由线段的性质,两点之间,线段最短,可知当-3≤x≤4时,|x+3|+|x-4|有最小值,从而可求得最小值,利用数轴即可找到此时x可取的整数值.
(2)把x与-1代入|a-b|即可得到答案;
(3)当-4<x<2时,根据绝对值的性质,即可化简|x-2|+|x+4|得到答案;
(4)求|x+3|+|x-4|的最小值,由线段的性质,两点之间,线段最短,可知当-3≤x≤4时,|x+3|+|x-4|有最小值,从而可求得最小值,利用数轴即可找到此时x可取的整数值.
解答:解:(1)|1-5|=4,
|2-(-1)|=3;
故答案为:4,3;
(2)|x-(-1)|=|x+1|;
故答案为:|x+1|;
(3)根据题意,可知当-4<x<2,时,
∴|x-2|=2-x,|x+4|=x+4,
∴|x-2|+|x+4|=2-x+x+4=6;
故答案为:6;
(4)根据题意,可知当-3≤x≤4时,|x+3|+|x-4|有最小值.
∴|x+3|=x+3,|x-4|=4-x,
∴|x+3|+|x-4|=x+3+4-x=7;
由数轴可知,-3≤x≤4的x的整数值为:-3,-2,-1,0,1,2,3,4.
|2-(-1)|=3;
故答案为:4,3;
(2)|x-(-1)|=|x+1|;
故答案为:|x+1|;
(3)根据题意,可知当-4<x<2,时,
∴|x-2|=2-x,|x+4|=x+4,
∴|x-2|+|x+4|=2-x+x+4=6;
故答案为:6;
(4)根据题意,可知当-3≤x≤4时,|x+3|+|x-4|有最小值.
∴|x+3|=x+3,|x-4|=4-x,
∴|x+3|+|x-4|=x+3+4-x=7;
由数轴可知,-3≤x≤4的x的整数值为:-3,-2,-1,0,1,2,3,4.
点评:本题主要考查绝对值,绝对值的性质,两点间的距离,读懂题目信息,理解数轴上两点间的距离的表示方法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
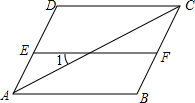 如图,AB∥CD,EF∥AB,且AC平分∠DAB,则图中与∠1相等的角有( )
如图,AB∥CD,EF∥AB,且AC平分∠DAB,则图中与∠1相等的角有( )| A、3个 | B、4个 | C、5个 | D、6个 |
 如图,已知∠1=40°,∠2=140°,∠3=40°,∠4=140°.试说明:a∥b,b∥c,d∥e,a∥c.
如图,已知∠1=40°,∠2=140°,∠3=40°,∠4=140°.试说明:a∥b,b∥c,d∥e,a∥c.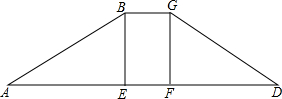 如图,水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1:3,斜坡CD的坡度i′=1:2.5.求斜坡AB的坡角α(精确到1度),坝底宽AD和斜坡AB的长(精确到0.1m)
如图,水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1:3,斜坡CD的坡度i′=1:2.5.求斜坡AB的坡角α(精确到1度),坝底宽AD和斜坡AB的长(精确到0.1m)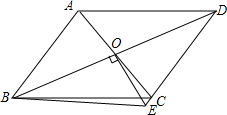 如图所示,?ABCD中,AC、BD相交于点O,OE⊥BD,交DC的延长线于E,连接BE,求证:∠ABD=∠EBD.
如图所示,?ABCD中,AC、BD相交于点O,OE⊥BD,交DC的延长线于E,连接BE,求证:∠ABD=∠EBD.