题目内容
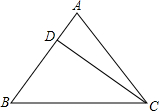 已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,
已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,(1)求证:CD⊥AB;
(2)求AD的长;
(3)求△ABC的周长.
考点:勾股定理的逆定理,等腰三角形的性质,勾股定理
专题:
分析:(1)首先根据BD、CD、BC长可利用勾股定理逆定理证明∠BDC=90°,进而得到CD⊥AB;
(2)设AD=xcm,则AB=AC=(x+12)cm,再利用勾股定理可得x2+162=(x+12)2,解方程可得x的值,即可求出AD的长;
(3)由(2)进而得到AB长,然后即可算出周长.
(2)设AD=xcm,则AB=AC=(x+12)cm,再利用勾股定理可得x2+162=(x+12)2,解方程可得x的值,即可求出AD的长;
(3)由(2)进而得到AB长,然后即可算出周长.
解答:解:(1)∵122+162=202,
∴DB2+CD2=BC2,
∴△BCD是Rt△,且∠BDC=90°,
∴CD⊥AB;
(2)设AD=xcm,则AB=AC=(x+12)cm,
∵∠BDC=90°,
∴∠ADC=90°,
∴x2+162=(x+12)2,
解得:x=
,
即AD的长为
;
(3)∵AD=
,
∴AC=AB=BD+AD=
,
∴△ABC的周长=AB+AC+BC=
×2+20=53
.
∴DB2+CD2=BC2,
∴△BCD是Rt△,且∠BDC=90°,
∴CD⊥AB;
(2)设AD=xcm,则AB=AC=(x+12)cm,
∵∠BDC=90°,
∴∠ADC=90°,
∴x2+162=(x+12)2,
解得:x=
| 14 |
| 3 |
即AD的长为
| 14 |
| 3 |
(3)∵AD=
| 14 |
| 3 |
∴AC=AB=BD+AD=
| 50 |
| 3 |
∴△ABC的周长=AB+AC+BC=
| 50 |
| 3 |
| 1 |
| 3 |
点评:此题主要考查了勾股定理,以及勾股定理逆定理,关键是掌握勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
 如图是一圆锥的侧面展开图,其弧长为10π,则该圆锥的全面积为 ( )
如图是一圆锥的侧面展开图,其弧长为10π,则该圆锥的全面积为 ( )| A、60π | B、85π |
| C、95π | D、169π |
 如图所示,点D在直线AB上,∠ADE=∠ABC,且DG,BF分别是∠ADE和∠ABC的平分线,那么DG一定平行于BF,为什么?
如图所示,点D在直线AB上,∠ADE=∠ABC,且DG,BF分别是∠ADE和∠ABC的平分线,那么DG一定平行于BF,为什么? 如图,在?ABCD中,E,F在AC边上,G,H在BD边上,且AE=CF,BH=DG,求证:EG∥HF.
如图,在?ABCD中,E,F在AC边上,G,H在BD边上,且AE=CF,BH=DG,求证:EG∥HF.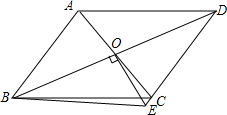 如图所示,?ABCD中,AC、BD相交于点O,OE⊥BD,交DC的延长线于E,连接BE,求证:∠ABD=∠EBD.
如图所示,?ABCD中,AC、BD相交于点O,OE⊥BD,交DC的延长线于E,连接BE,求证:∠ABD=∠EBD.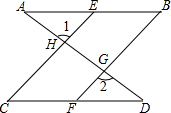 如图,直线AD与AB,CD相交于A,D,两点,EC,BF,与AB、CD相交于点E,C,B,F,如果∠1=∠2,∠B=∠C.小明在图上把两组相等角的信息标注出来后,略加分析,便发现CE∥BF,同桌的小慧说:“不光有这个发现,我还能得到∠A=∠D呢.”小明在深入其中,很快也明白了小慧是怎样得到∠A=∠D的了.你能帮助他们写出过程吗?
如图,直线AD与AB,CD相交于A,D,两点,EC,BF,与AB、CD相交于点E,C,B,F,如果∠1=∠2,∠B=∠C.小明在图上把两组相等角的信息标注出来后,略加分析,便发现CE∥BF,同桌的小慧说:“不光有这个发现,我还能得到∠A=∠D呢.”小明在深入其中,很快也明白了小慧是怎样得到∠A=∠D的了.你能帮助他们写出过程吗? 如图,a∥b,m∥n,∠1=35°,则∠2等于多少度?
如图,a∥b,m∥n,∠1=35°,则∠2等于多少度?