题目内容
20.已知直线y=mx-1上有一点P(1,n)到原点的距离为$\sqrt{10}$,则直线与两轴所围成的三角形面积为$\frac{1}{4}$或$\frac{1}{8}$.分析 先根据点(1,n)到原点的距离是$\sqrt{10}$求出n的值,故可得出此点坐标,把此点坐标代入直线y=mx-1即可得出直线的解析式,由此可得出此直线与两坐标轴围成的三角形面积.
解答 解:∵点B(1,n)到原点的距离是$\sqrt{10}$,
∴n2+1=10,即n=±3.
∴(1,±3),
∴一次函数的解析式为:y=4x-1或y=-2x-1.
当一次函数的解析式为y=4x-1时,与两坐标轴围成的三角形的面积为:$\frac{1}{2}$×$\frac{1}{4}$×1=$\frac{1}{8}$;
当一次函数的解析式为y=-2x-1时,与两坐标轴围成的三角形的面积为:$\frac{1}{2}$×$\frac{1}{2}$×1=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$或$\frac{1}{8}$.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
9.6月30日以来的强降雨造成某地洪灾.某市组织20辆汽车装运食品、药品和生活用品三种物质共100吨前往灾区.按计划20辆汽车都要装运,且每辆汽车只能装运同一种物质,且必须装满.根据下表提供的信息,解答下列问题.
(1)设装运食品的车辆数为x,装运药品的车辆数为y,求y与x的函数关系式;
(2)如果装运食品的车辆数不少于5辆,装运药品的车辆数不少于4辆,那么有几种车辆安排方案?请写出所用的方案.
| 物资种类 | 食品 | 药品 | 生活用品 |
| 每辆汽车运载量(吨) | 6 | 5 | 4 |
(2)如果装运食品的车辆数不少于5辆,装运药品的车辆数不少于4辆,那么有几种车辆安排方案?请写出所用的方案.
 如图,平面直角坐标系xOy中,点A(a,1)在双曲线上y=$\frac{3}{x}$上,函数y=kx+b的图象经过点A,与y轴上交点B(0,-2),
如图,平面直角坐标系xOy中,点A(a,1)在双曲线上y=$\frac{3}{x}$上,函数y=kx+b的图象经过点A,与y轴上交点B(0,-2),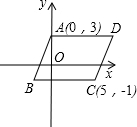 如图所示,在平面直角坐标系中,AD∥BC∥x轴,AD=BC=7,A(0,3),C(5,-1).
如图所示,在平面直角坐标系中,AD∥BC∥x轴,AD=BC=7,A(0,3),C(5,-1).