题目内容
16.已知a-b=3,a-c=1,求a2+b2+c2-ab-ac-bc的值.分析 先把原式变形得到原式=$\frac{1}{2}$(a2+b2-2ab)+$\frac{1}{2}$(b2+c2-2bc)+$\frac{1}{2}$(a2+c2-2ac),再利用完全平方公式得到原式=$\frac{1}{2}$(a-b)2+$\frac{1}{2}$(b-c)2+$\frac{1}{2}$(a-c)2,由于a-b=3,a-c=1,则b-c=-2,然后利用整体思想进行计算.
解答 解:∵a-b=3,a-c=1,
∴b-c=-2,
∴a2+b2+c2-ab-ac-bc
=$\frac{1}{2}$(a2+b2-2ab)+$\frac{1}{2}$(b2+c2-2bc)+$\frac{1}{2}$(a2+c2-2ac)
=$\frac{1}{2}$(a-b)2+$\frac{1}{2}$(b-c)2+$\frac{1}{2}$(a-c)2
=$\frac{9}{2}$+2+$\frac{1}{2}$
=7.
点评 本题考查了因式分解的应用:利用因式分解的方法把所给的代数式和等式进行变形,然后得到更为简单的数量关系,再利用整体思想解决问题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
6.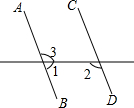 如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是( )
如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是( )
 如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是( )
如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是( )| A. | ∠2=70° | B. | ∠2=100° | C. | ∠2=110° | D. | ∠3=110° |
4.下列各式计算正确的是( )
| A. | (-5an+1b)(-2a)=-10an+2b | B. | (-4a2b)(-a2b2)($\frac{1}{2}$b3c)=2a4b6c | ||
| C. | (-3xy)(-x2z)6xy2=3x3y3z | D. | (2anb3)(-$\frac{1}{6}$abn-1)=-$\frac{1}{3}$an+1b3n-3 |
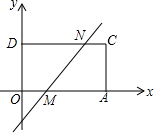 点A的坐标是(4,0),点M是OA上一点,且AM=3OM,把点A向上平移2个单位到点C,过点C作y轴的垂线,垂足为点D.
点A的坐标是(4,0),点M是OA上一点,且AM=3OM,把点A向上平移2个单位到点C,过点C作y轴的垂线,垂足为点D.