题目内容
7.已知关于x的方程x2+2(a-1)x+a2-7a-4=0的两根为x1、x2,且满足x1x2-3x1-3x2-2=0.则(1+$\frac{4}{{a}^{2}-4}$)•$\frac{a+2}{a}$的值是2.分析 根据根与系数的关系得到x1+x2=-2(a-1),x1•x2=a2-7a-4,利用x1x2-3x1-3x2-2=0得a2-7a-4+6(a-1)-2=0,解得a1=4,a2=-3,再把(1+$\frac{4}{{a}^{2}-4}$)•$\frac{a+2}{a}$化简得到$\frac{a}{a-2}$,然后根据分式有意义的条件得到a=4,然后把a=4代入计算即可.
解答 解:根据题意得x1+x2=-2(a-1),x1•x2=a2-7a-4,
∵x1x2-3x1-3x2-2=0,
∴a2-7a-4+6(a-1)-2=0,
整理得a2-a-12=0,解得a1=4,a2=-3,
(1+$\frac{4}{{a}^{2}-4}$)•$\frac{a+2}{a}$=$\frac{{a}^{2}-4+4}{(a+2)(a-2)}$•$\frac{a+2}{a}$
=$\frac{a}{a-2}$,
∵a-2≠0,
∴当a=4时,(1+$\frac{4}{{a}^{2}-4}$)•$\frac{a+2}{a}$=$\frac{4}{4-2}$=2.
故答案为2.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.也考查了分式的化简求值.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
18.小红在报纸上看到淡水资源的一份报道,世界人均可再生淡水资源6521立方米,中国人均可再生淡水资源仅2134立方米,淡水消费分三类:农业用水、工业用水、生活用水,三类淡水消费所占百分比如图所示:

图中只有世界淡水消费中农业用水的百分比为82.5%,其余百分比都看不清了,但报纸中说到在淡水消费中:中国工业用水所占百分比是世界工业用水所占百分比的3倍还多3.8个百分点,中国农业用水所占百分比比中国工业用水所占百分比多42个百分点,中国生活用水所占百分比比世界生活用水所占百分比少3.6个百分点.请利用列二元一次方程组计算出三类淡水消费其余各项百分比,写出完整的解答题并填写到统计表中.

图中只有世界淡水消费中农业用水的百分比为82.5%,其余百分比都看不清了,但报纸中说到在淡水消费中:中国工业用水所占百分比是世界工业用水所占百分比的3倍还多3.8个百分点,中国农业用水所占百分比比中国工业用水所占百分比多42个百分点,中国生活用水所占百分比比世界生活用水所占百分比少3.6个百分点.请利用列二元一次方程组计算出三类淡水消费其余各项百分比,写出完整的解答题并填写到统计表中.
| 三类淡水消费所占百分比 | |||
| 农业用水 | 工业用水 | 生活用水 | |
| 世界 | 82.5% | 7.3% | 10.2% |
| 中国 | 67.7% | 25.7% | 6.6% |
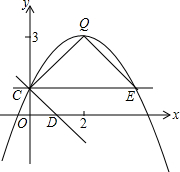 如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC
如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC